Interpolation is the process of mapping a variable V_0 at unsampled locations using a set of samples of known location and V_0 value (Fig. 1). These samples can come from a field campaign or can be the information measured by fixed or mobile sensors inside a field. More than often, in Precision Agriculture studies, one has a subset of information within a field (the samples) and wants to derive a map of this information over the entire field. In general, only samples are available because field campaigns are cumbersome and time-consuming or because the deployment of too many sensors would be really expensive. Of course, it would no be possible to collect information at every square centimeter inside the field. That is why interpolation methods are of interest. Many interpolation techniques exist but it is sometimes difficult to understand the advantages and flaws of each approach. This post intends to provide an overview of the most common interpolation methods.

Figure 1. Interpolation principle
Spatial interpolation techniques can be divided into two main categories : deterministic and geostatistical approaches. To put it simple, deterministic methods do not try to capture the spatial structure in the data. They only make use of predefined mathematical equations to predict values at unsampled locations (by weighing the attribute values of samples with known location). On the contrary, geostatistical approaches intend to fit a spatial model to the data. This enables to generate a prediction value at unsampled locations (like deterministic methods) and to provide users with an estimate of the accuracy of this prediction. Deterministic methods gather the TIN, IDW and Trend surface analysis techniques. Geostatistical approaches include kriging and its variants. All the methods that will be discussed have to be applied on continuous variables (ex: NDVI, yield, soil carbon content…) and not factorial (ex: a class arising from a classification-based method) or binomial variables (variables with a value of 0 or 1 – there are some kriging methods that tackle this type of data – Indicator Kriging for instance – but we won’t talk about it here).
Interpolation techniques rely on the fact that spatial datasets exhibit some spatial correlation. In fact, everything is related to everything else, but near things are more related than distant things (Tobler, 1970) 1. Interpolation methods can be used to predict values at specific locations in the field or over a whole grid of interpolation. In this case, this grid is made of regularly-spaced pixels whose size can depend on the desired accuracy of the interpolated map or on the spatial structure of the dataset.
TIN : Triangular Interpolation Network
The TIN technique is maybe one of the most simple spatial interpolation technique. This approach relies on the construction of a triangular network (a specific-case of tesselation) based on the samples spatial location. Multiple triangulation methods might be used to create the network but that of Delaunay is the most commonly reported (Fig. 2). This method aims at creating non-overlapping triangles (as equilateral as possible) whose circumscribed circle contains only the three points that gave birth to the triangle. Once the network is operational, each new position z_i where an attribute value needs to be predicted is associated to the triangle T in which it lies. The attribute value at z_i is calculated as a weighing of the values of the three apexes of the triangle T
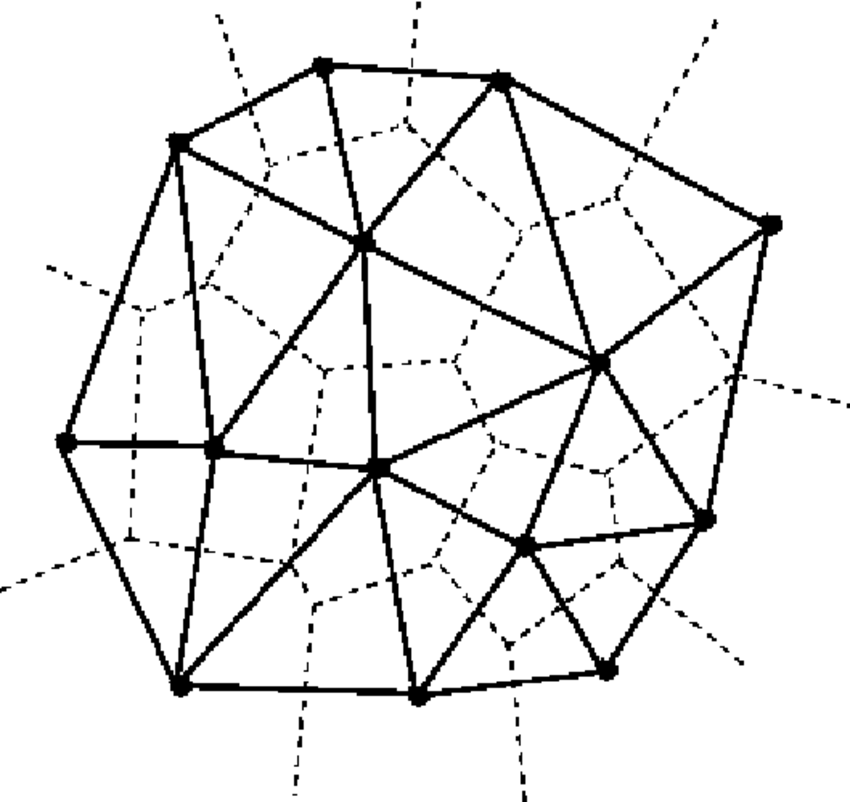
Figure 2. Creation of a triangular network : the Delaunay triangulation
It is clear that the accuracy of the method is strongly dependent on the number of observations within the field, and more especially about the density of observations. When samples are clustered, neighbouring observations will be given a relatively good prediction. On the contrary, for isolated samples, the constructed triangle will be much larger and the prediction will be even more imprecise or flawed. Remind that each predicted value only depends on the three apexes of a triangle. This method might be problematical when small scale variations are present.
For instance, the interpolation of elevation values by the TIN technique might generate some discontinuous areas due to abrupt elevation variations (discontinuities, slope) which are not realistic.
Effectively, this interpolation technique does not smooth the data. The TIN technique is available on many softwares and is really efficient from a computation time point of view. It might be applied when lots of observations are available without requiring important memory storage. Note that the network that has been created is also interesting to provide an indication of the influence area of each observation. In that case, other tesselations such as the Thiessen polygons are of particular interest.
IDW : Inverse Distance Weighing
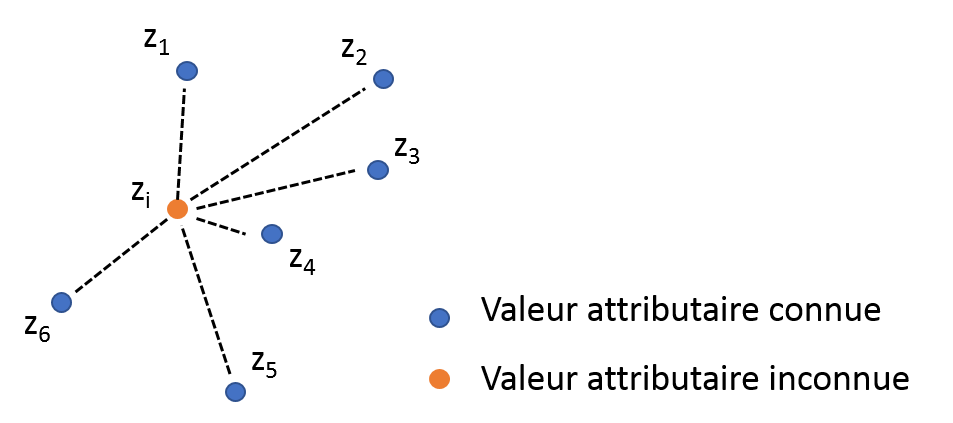
Figure 3. Inverse distance weighing.z_4 has more influence on the attribute value of Ai than z_2 and z_3 because A1 is the nearest to Ai.
As the name suggests, the IDW technique predicts attribute values at unsampled locations based on the spatial distance of known observations from these unsampled locations (Fig. 3). The nearest observations to the unsampled locations are given the larger weights while very distant observations have a relatively low influence on the prediction. The weight attributed to each known observation is controlled by a power parameter, often referred to as p. As p increases, the weight attributed to distant observations decreases. This factor can be considered as a smoothing parameter. If the smoothing effect is to important, it might blur some interesting variations or make the variable look much more homogeneous than it actually is. In fact, if p is small, neighbouring and distant observations exercise a strong influence on unsampled locations. As a consequence, the prediction might be heavily smoothed because it does not solely consider local processes. On the other hand, if p is set too high, only the very local phenomena will be accounted for and the interpolated map might present a jagged appearance. One advantage over the TIN technique is that the IDW approach involves more observations into the prediction at unsampled locations, which is likely to be more beneficial for its accuracy. However, one has to set properly the p parameter so that the interpolated map is considered reliable. Like the TIN method, the IDW technique is relatively easy to compute and is widely available among common softwares (QGIS, ArcGIS, SAGA GIS…) and languages (R, Python, Matlab).
Trend Surface Analysis
Trend surface analysis intend to fit a trend to the data. In other words, the objective is to find the equation that best matches with the attribute values of the available data. Trend surface analysis often involves multiple linear regressions or polynomial functions to find a relationship between the predicted variable and a combination of the spatial coordinates. Polynomial functions can sometimes be relatively complex, with a 4 or 5 order (y=aX^{4}+bX^{3}+cX^{2}).
This approach is a global technique because it considers all the data available to put into place the linear regressions or the polynomial functions. More local approaches could be implemented to improve the prediction accuracy. Note that the trend surface analysis can suffer from outlying values. In fact, an abnormal observation is likely to severely influence the proposed model and might lead to a really bad fit to the data. To make the trend surface analysis more reliable, there is a need to calibrate and then to validate the selected regressions or polynomial functions. Indeed, a subset of the samples should be used to infer a specific model and then, a independent set of samples (or at least the remaining samples in the initial set) should be used to validate the proposed model. The use of both training and validation datasets is fundamental to evaluate the reliability and accuracy of the proposed model.
All the aforementioned deterministic approaches are widely reported and used because they are relatively simple to understand and easy to compute. However, all these methods only account for the spatial distance between observations to make the predictions. None of them intend to capture the spatial structure in the data or the spatial patterns that might be present within the fields. The fact that no spatial model is put into place makes it not possible to have an idea of the accuracy of the predictions over the whole field. As it was stated for the trend analysis approach, by making use of model validation procedures, it is possible to know the prediction accuracy of the model but only at the known sampling locations. It is not possible to derive it for the entire interpolated maps. Contrary to these deterministic methods, geostatistical techniques enable to compute an error map to spot the locations where the predictions are accurate and other where the predictions are flawed.
Kriging
Kriging is the most commonly used geostatistical approach for spatial interpolation. Kriging techniques rely on a spatial model between observations (defined by a variogram) to predict attribute values at unsampled locations. One of the specificity of kriging methods is that they do not only consider the distance between observations but they also intend to capture the spatial structure in the data by comparing observations separated by specific spatial distances two at a time. The objective is to understand the relationships between observations separated by different lag distances. All this knowledge is accounted for in the variogram. Kriging methods then derive spatial weights for the observations based on this variogram. It must be noted that kriging techniques will preserve the values of the initial samples in the interpolated map.
Kriging methods consider that the process that originated the data can be divided into two major components : a deterministic trend (large scale variations) and an autocorrelated error (the residuals).
Z(s)=m+e(s)
Where Z(s) is the attribute value at the spatial position s, m is the deterministic trend that does not depend on the location s of the observations and e(s) is the autocorrelated error term (which depends on the spatial position s). Note that the trend is deterministic ! The variogram is only computed on the residuals which are supposed to exhibit a spatial correlation ! Basically, when someone intends to fit a variogram model to the data, it actually tries to fit this model to the residuals of the data, after the trend is removed. Be aware that, depending on the shape of the variogram, the resulting interpolated map can be heavily smoothed. In fact, if the nugget effect of the variogram is strong, kriging techniques will tend to smooth the data to blur the noise within the fields. It is sometimes surprising because the range of values after kriging can be smaller than that of the samples. If the nugget component is effectively very high regarding the partial sill, the spatial structure might be relatively poor and it would be better not to interpolate. Many variants of kriging depends on the way the trend is characterized. This will be discussed later.
Thanks to the computation of the variogram, an error map can be derived on the entire field because the relationships between any two observations separated by a distance h is known. The error map is a very useful tool because it make access the to the prediction accuracy of the interpolated map. Be aware that the quality of the error map obviously relies on the quality of the model fitting to the variogram. If a variogram model fits poorly to the data, the error map might be questionable. Be aware that the interpolation by any kriging techniques is sensitive to outliers. Here, abnormal observations might mask the data autocorrelation and prevent the spatial structure from being determinated. The intuitive solution would be to remove these outlying values before kriging. However, it can happen that some values look like they are abnormal because they are much higher or lower than the remaining values in the dataset. If these observations are clustered, this so-called outliers might be due to a real phenomenom. In order to account for this specificity and not deleting abruptly these outliers, one solution would be to compute the variogram without these observations but perform kriging with them. As such, the spatial structure would still be defined and these extreme observations would be kept inside the dataset.
Simple kriging
As the name suggests, simple kriging is the most simple kriging variant. In this case, the deterministic trend, m, is known and considered constant over the whole field under study (Fig. 4).
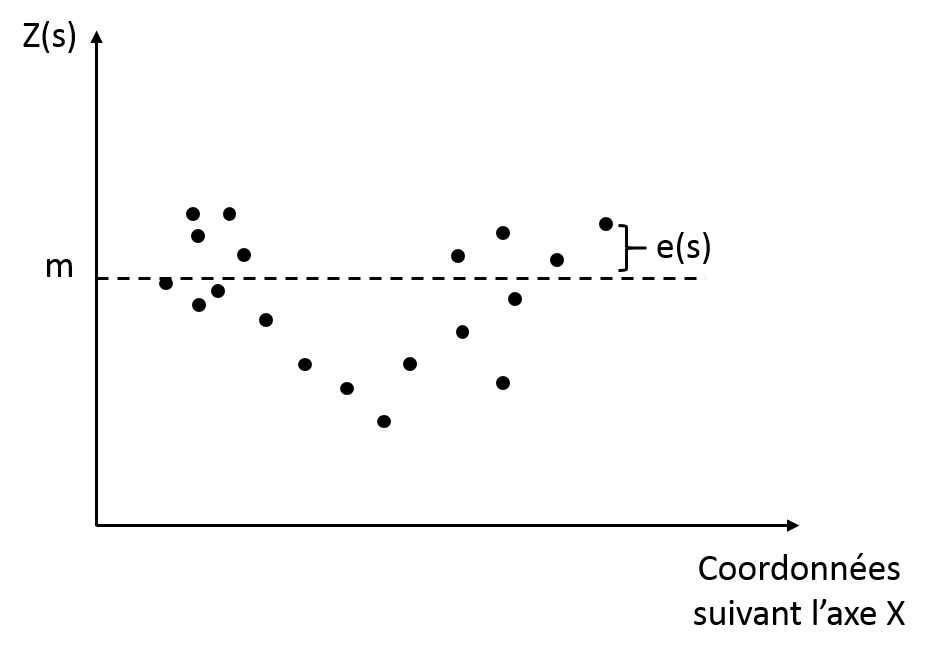
Figure 4. Simple kriging and corresponding trend and residuals
This method is global because it does not account for local variations of the trend. However, if there is no abrupt changes of the variable of interest (or if there is no reason there would be one), this assumption can be viable and relevant. As the trend is considered known, the autocorrelated terms are also known which makes the prediction more simple. It must be understood that, here, predicted values cannot extend beyond the range of the sample values.
Ordinary kriging
This technique is the most reported kriging approach. Contrary to simple kriging, this method considers that the trend is constant but only within a local neighbourhood (Fig. 5). This assumption is interesting because it ensures to account for the local variations within the field.
One could imagine for instance a break in slope within a field that could be interesting to consider
Ordinary kriging can be expressed as such :
Z(s)=m(s)+e(s)
Here the trend depends on the spatial location of the observation (m(s)).
This constant trend is assumed unknown here and has to be derived from the data in the according neighbourhood.
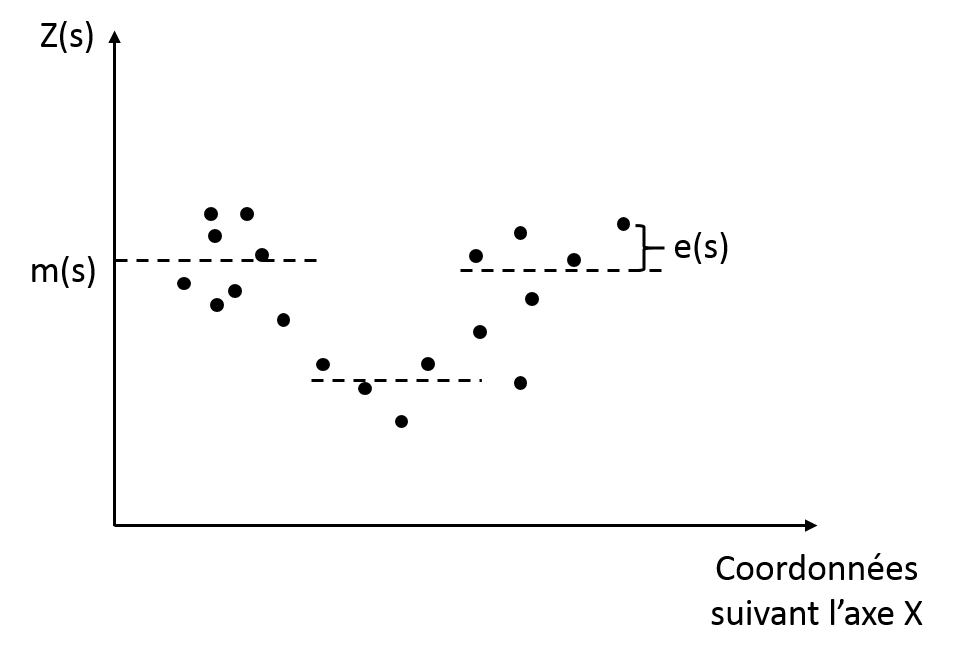
Figure 5. Ordinary kriging and corresponding estimated trend and residuals
As such, there is a need to define the extent of the neighbourood : the number of neighbouring observations that will be taken into account for each prediction. As the trend is considered unknown, it may happen that, by construction, the range of the predicted values extend beyond the range of the sample values.
Regression kriging or kriging with an external drift
Regression kriging has multiple names : universal kriging or kriging with an external trend. It is similar to ordinary kriging in the way that it considers that the determinitic trend is not constant over the whole field but depends on the spatial location of the observation. However, here, the trend is modelled by a more complex function, it is not simply considered constant over a neighbourhood (Fig. 6). The objective is the same as before : detrend the data so that the autocorrelated residuals can be studied. At the end of the interpolation, the trend is added back to the interpolated residuals.
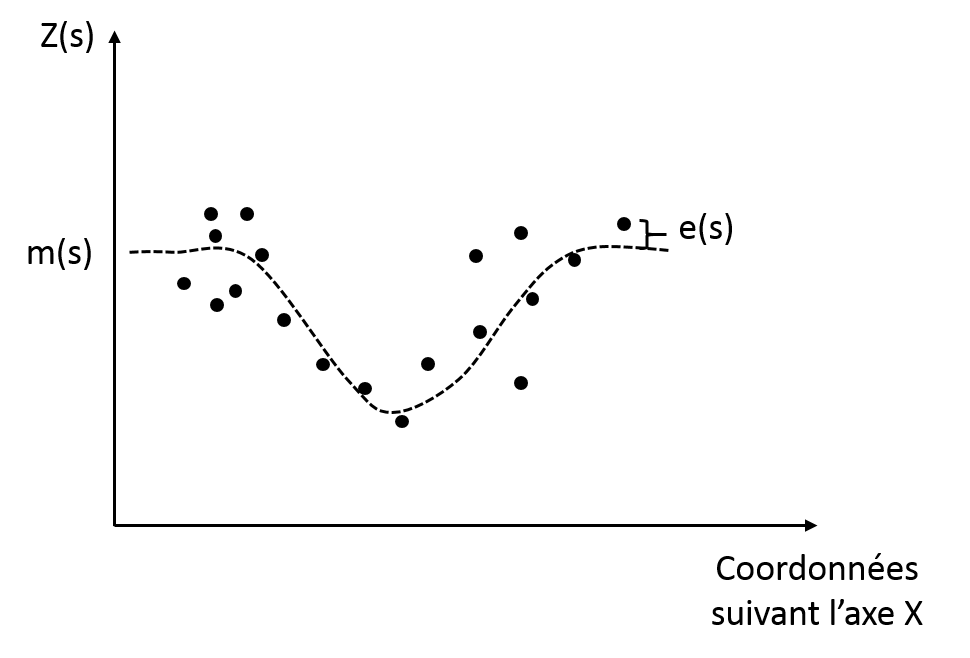
Figure 6. Regression kriging with corresponding trend and residuals
Regression-kriging is interesting when one possesses high spatial resolution auxiliary data and would like to have more information about a second variable from which he only has samples. In general, this second variable is cumbersome, expensive and/or time-consuming to obtain. In that case, the objective is to model the relationship between this second variable and the auxiliary data in order to improve the prediction of the secondary variable at unsampled locations.
For example, biomass information is relatively easy to acquire (via vegetation indexes such as NDVI obtained with satellite or UAV images). One could use this auxiliary variable to help interpolate the yield values available at a much lower spatial resolution (estimated at specific locations during a field campaign)
Note that if the relationship between the two variables is low, the regression kriging will be similar to an ordinary or a simple kriging approach.
Co-kriging
When one disposes of a high spatial resolution auxiliary variable V0 and wants to capture the spatial variability or correlation of a second variable V1, co-kriging is of particular interest. In fact, the objective is to evaluate the spatial structure of V1 regarding V0 with the samples available and then interpolate this spatial structure at unsampled locations. At previously stated, V1 is generally time-consuming and or expensive to obtain and it is much easier to make use of auxiliary data to improve the prediction of V1 at unsampled locations. Co-kriging requires the user to compute a cross-variogram and to fit a variogram model to it. In this case, the objective is not to evaluate the evolution of the variance of a given variable for increasing distance lags between observations but to study the evolution of the covariance of V1with respect to V0 for increasing distance lags between observations. In other words, how the spatial structure of V1 evolves regarding V0. It can be added that the cross-variogram is also an interesting tool to characterize whether two variables are spatially correlated or share the same spatial structure. In this later case, the two variables can be of high spatial resolution and the objective might no be to interpolate them. Co-kriging is more difficult to implement than the other kriging techniques but it might result in better predictions if it is performed correctly.
Point kriging / Block-kriging
All the aforementioned kriging techniques aim at predicting the value of a variable at specific unsampled locations. These locations can be considered as spatial points (or more precisely as pixels in the grid of interpolation). As a consequence, these kriging approaches are also referred to as point kriging methods. When the uncertainty is relatively large, one might want to smooth the interpolated results by performing kriging on a larger area than single pixels. This type of kriging interpolation is known as block kriging. This has the advantage of lowering prediction errors over the map. Obviously, it comes with the risk of loosing some useful information but when the uncertainty is too important, it might be worth it.
Before finishing this post, it must be mentioned that all the interpolation techniques that were presented generate relatively similar results in ideal cases (large number of observations available, non-noisy datasets and not abrupt variations within the fields). However, when the previous conditions are not met, geostatistical methods are interesting because they enable to embrace the spatial structure over the whole field, thus conditioning better predictions. These methods are harder to implement because there is a need to derive a spatial model of the data, but they might result in a better characterization of the field. Once again, I would not recommend to apply kriging methods without manual supervision because results could be surprising if the spatial model is not fit appropriately to the data. When the spatial structure is relatively poor (the noise is important), all interpolation approaches will smooth the data to a greater or lesser extent. This must be kept in mind before interpolating spatial observations because interpolated maps might appear much more homogeneous than they really are. It must be added that interpolation techniques can also be used to downsample (most often) or upsample an image or a map. The objective is to change the resolution of the map available.
For instance, if a NDVI image is acquired with a spatial resolution of 50cm, one might be interested in downsampling the resulting image to a spatial resolution of 5m to smoother representation of the interpolated map
Support Aspexit’s blog posts on TIPEEE
A small donation to continue to offer quality content and to always share and popularize knowledge =) ?


Great piece…
very insightful, thanks so much