Les outils d’agriculture de précision (capteurs piétons, statiques, embarqués sur tracteurs ou vecteurs aéroportés…) permettent d’acquérir des jeux de données agronomiques et environnementaux à des résolutions spatiales, temporelles, et attributaires impressionnantes. Et d’une manière générale, nous avons tendance à faire confiance à ces données captées (parfois trop), c’est-à-dire que nous les utilisons souvent telles quelles, sans vraiment trop se poser de questions ! Ces données sont pourtant souvent entachées d’incertitude, et il y est important d’y faire attention ! Qu’elles que soient les incertitudes, le plus important lorsqu’on s’attelle à analyser des données est d’être capable de lister, caractériser et quantifier les incertitudes, de manière à bien clarifier la confiance que l’on va pouvoir accorder aux données avant de prendre notre décision finale.
Différentes sources d’incertitude
Assez simplement, on peut classer les incertitudes en deux grandes catégories :
- Les incertitudes non aléatoires (épistémiques): Ce sont les incertitudes sur lesquelles on peut considérer qu’on a la main ou que l’on pourrait réduire, par exemple si on avait une meilleure connaissance des systèmes/cultures que l’on étudie, si l’on disposait de capteurs plus précis et/ou mieux étalonnés, ou encore si l’on utilisait des procédures plus robustes et fiables
Et on peut trouver plein d’exemples : capteur de rendement mal étalonné (incertitude sur la valeur attributaire de rendement en sortie du capteur), récepteur GNSS peu fiable (incertitude sur le positionnement dans l’espace d’une mesure issue d’un capteur embarqué), peu d’échantillons de sol (incertitude sur la représentativité des mesures à l’échelle de la parcelle), zones de productivité délimitées de manière experte par un agriculteur ou un conseiller (incertitude sur les limites/frontières exactes des zones), modèle agronomique pas exactement parfait [c’est de toute manière impossible] (incertitude sur les sorties du modèle)….
- Les incertitudes aléatoires (naturelles): Ce sont, au contraire, les incertitudes qui ne sont pas réductibles parce qu’elles sont la consequences de processus que nous ne pouvons pas maitriser
Encore une fois, quelques exemples en agriculture de précision : la volatilité du prix d’achat d’intrants ou du cours d’une céréale (incertitude sur le chiffre d’affaire, les charges fixes et variables de l’exploitation), les conditions climatiques à moyen/long terme (incertitude sur l’impact d’une décision à un instant « t1 » sur le résultat à l’instant « t2 »), la variabilité intrinsèque ou naturelle des plantes (incertitude sur la valeur d’un paramètre agronomique d’une plante lorsque l’on a mesuré ce même paramètre très précisément sur une plante extrêmement proche dans l’espace).
Analyse d’incertitude
Toutes les données que l’on collecte vont généralement être intégrées et compilées dans un modèle (qu’il soit expert, mathématique ou que sais-je) qui va amener à une prise de décision. Quand on parle d’analyse d’incertitude, on essaye en fait de connaitre l’incertitude de notre variable de sortie de modèle. Par exemple, si je suis céréalier, mon chiffre d’affaires est incertain (parce qu’il y a beaucoup d’incertitudes comme on l’a vu précédemment) mais j’aimerais quand même bien avoir une idée de la distribution probable de mon chiffre d’affaires. Pour avoir cette distribution, il faut donc que je prenne en compte toutes les données nécessaires au calcul de mon chiffre d’affaires (mes données d’entrée) et les incertitudes associées. Il va donc falloir à un moment où un autre, que je modélise ces incertitudes de manière à pouvoir les prendre en compte de manière un peu plus objective. Sans entrer dans le détail, on peut imaginer plusieurs approches de modélisation.
La première, très simple, est de raisonner par scénario. C’est une approche que l’on peut imaginer quand on n’a pas vraiment d’idée sur le niveau d’incertitude à prendre en compte pour notre donnée d’intérêt (dans le cadre d’une variabilité aléatoire par exemple). L’approche consiste donc à proposer plusieurs scénarios (on n’a pas beaucoup avancé…) possibles pour la donnée d’entrée que l’on cherche à évaluer. Prenons l’exemple de la donnée d’entrée « cours des céréales » et de son incertitude associée, la « volatilité des prix ». Je peux imaginer un premier scénario où je vendrais mon blé à 150€ la tonne, et un deuxième où je la vendrais à 200 € la tonne. On utilise ici des scénarios ponctuels. Je peux donc très bien imaginer un scénario catastrophe (prix à la tonne très bas) ou scénario avantageux (prix à la tonne très haut) pour évaluer l’incertitude de mon chiffre d’affaires. Je peux aussi aller plus loin en imaginant un scénario moyen, qui prendrait en compte la moyenne du cours du blé sur 10 ans.
La deuxième, un peu plus avancée, est de raisonner de façon probabiliste. L’idée est ici de proposer des scénarios continus de probabilité pour la donnée que l’on cherche à évaluer. Mais cette approche demande d’avoir quand même un peu plus une idée de la tête de notre incertitude. Sur le même exemple que précédemment, si je connais l’historique du cours du blé sur 20 ans, je peux construire une loi de probabilité du cours de blé et donc mettre en avant le fait que des scénarios sont plus probables que d’autres.
Pour évaluer la distribution probable de mon chiffre d’affaires, je vais donc pouvoir calculer plein de chiffres d’affaires différents en utilisant, pour chaque itération, un cours du blé dont la valeur aura été tirée dans les scénarios ou la loi de probabilité que j’aurais mise en place (plusieurs outils existent pour tirer dans ces lois de probabilités, par exemple la méthode de Monte Carlo). A la fin de mes itérations, j’aurai donc une distribution (que je peux essayer de modéliser ou approximer si j’en ai envie) qui me montrera la variabilité de ma variable de sortie (mon chiffre d’affaires) en fonction de ma variable d’entrée (cours du blé). On aura donc réalisé l’analyse d’incertitude de notre chiffre d’affaires. L’exemple pris ici est très simplifié parce que l’on a regardé qu’une seule variable d’entrée mais il est totalement extensible à un grand nombre de variables d’entrée. Il y a néanmoins quelques précautions à prendre quand on commence à travailler sur l’incertitude (que ce soit sur une ou plusieurs variables), notamment pour des notions de corrélations entre individus ou variables.
Connaitre l’incertitude associée à notre variable de sortie, c’est intéressant, certes. Mais il est quand même plus pertinent de connaitre les paramètres d’entrée qui vont avoir le plus d’influence sur cette variable de sortie. C’est vrai que si un paramètre d’entrée influence peu la variable de sortie (et donc son incertitude), il n’y a pas énormément d’intérêt à passer du temps dessus. C’est ce qu’on va voir dans la partie suivante avec l’analyse de sensibilité !
Un focus sur l’analyse de sensibilité
L’analyse de sensibilité a pour objectif d’évaluer l’importance des paramètres d’entrées d’un modèle sur les variables d’intérêt de sortie de ce modèle. Cela va donc permettre de regarder les paramètres sur lesquels se focaliser pour diminuer l’incertitude associée à notre variable de sortie. L’analyse de sensibilité permet de répondre aux questions du type : Quels sont les paramètres d’entrée les plus impactants de mon modèle ? Quelle part de la variabilité de mon modèle est expliqué par le paramètre d’entrée X ? Comment la variabilité des données d’entrée d’un modèle impacte la variabilité de la réponse de sortie de ce modèle ?
Les méthodes d’analyse de sensibilité sont principalement de trois types :
- Les méthodes dites « de criblage » (ex : Morris) cherchent à évaluer l’influence des paramètres d’entrée d’un modèle, en faisant varier ces paramètres un par un (Morris fait partie des méthodes dites OAT, One At a Time). Ce sont des méthodes adaptées lorsqu’il y a beaucoup de paramètres d’entrée parce qu’elles permettent de faire ressortir plus rapidement les paramètres d’influence que les méthodes dites « globales » qui sont, elles, très demandeuses en temps de calcul.
- Les méthodes dites « locales » cherchent à évaluer à quel point une faible variation des valeurs d’un paramètre d’entrée d’un modèle influence les sorties de ce modèle. Ces méthodes sont locales parce qu’elles ne s’intéressent pas à l’ensemble des valeurs possibles que peut prendre le paramètre d’entrée mais seulement à des variations locales autour d’une valeur cible,
- Les méthodes “globales”, au contraire, s’intéressent à la variabilité de la sortie du modèle dans l’intégralité de son domaine de variation. Les méthodes les plus couramment utilisées (méthodes de Sobol et Fast), se basent sur une approche de décomposition de variance pour représenter la proportion de la variabilité du modèle expliquée par une entrée ou un groupe d’entrée du modèle
Exemple :
Récemment, j’ai travaillé sur l’analyse de sensibilité d’un modèle de préconisation en fumure de fonds à ses paramètres d’entrée (notamment en rapport avec des analyses d’échantillons de sols en laboratoire, l’interprétation de ces analyses de terre en classes expertes, les pratiques agricoles réalisées et/ou envisagées ou encore le niveau de production passé et l’objectif de production de la culture à venir). Dans cette étude, l’analyse de sensibilité avait été réalisée avec la méthode globale de Sobol, et ce pour plusieurs raisons. Dans la mesure où le modèle utilisait certaines données qualitatives (ex : stratégie de fertilisation, devenir des résidus de culture…), j’avais choisi de privilégier des méthodes globales parce que les méthodes « locales » ne pouvaient pas être appliquées (Etudier les variations locales d’une variable non continue n’avait pas vraiment de sens) et les méthodes de criblage de type « Morris » n’étaient pas très adaptées non plus. Les méthodes de Sobol, pour leur part, sont intéressantes à plusieurs titres. Elles permettent tout d’abord de s’affranchir de cette précédente contrainte sur les variables qualitatives. Deuxièmement, ces méthodes génèrent des indices facilement interprétables (les indices de Sobol) pour exprimer la proportion de variance du modèle expliquée par les variables d’entrée. Enfin, les méthodes de Sobol permettent de caractériser non seulement l’impact d’un paramètre seul sur le modèle mais aussi les interactions entre ce paramètre et les paramètres restants. Il est par exemple tout à fait envisageable qu’un paramètre seul n’ait pas beaucoup d’importance mais que ce soit son interaction avec d’autres paramètres d’entrée du modèle qui lui confère de l’intérêt (Figure 1)
Une des hypothèses importantes à respecter pour ne pas biaiser les résultats d’une analyse de sensibilité est de s’assurer que les variables d’entrée du modèle ne soient pas corrélées entre elles. Force est de constater que certains paramètres du modèle l’étaient ! C’était par exemple le cas entre l’espèce cultivée et son rendement (deux espèces différentes n’auront pas forcément le même niveau de rendement) ou encore entre un type de sol et ses teneur initiale en P/K (certains types de sol auront toujours une teneur en P/K inférieure à d’autres types de sol). Pour limiter les effets de corrélation entre variables, les analyses de sensibilité avaient été réalisées par type de sol et par culture.
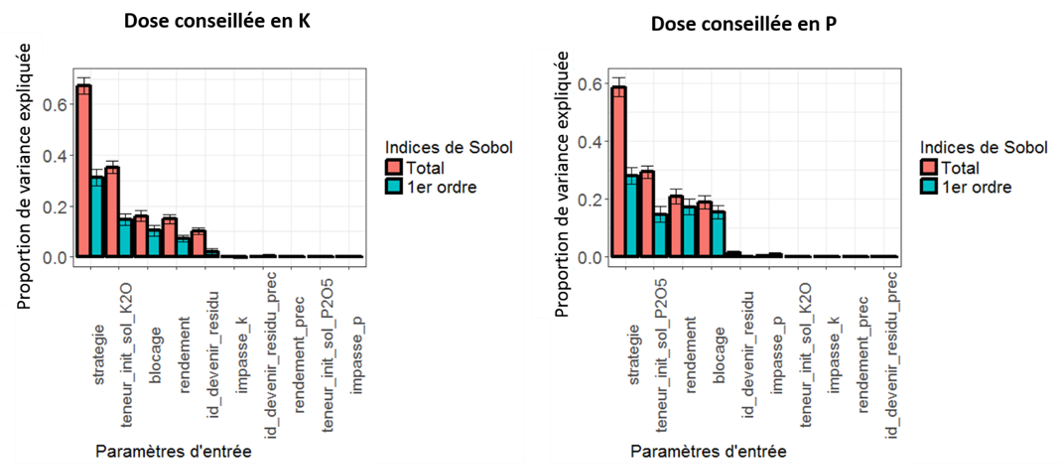
Figure 1. Analyse de sensibilité d’un modèle agronomique de fumure de fonds
Les analyses d’incertitude et de sensibilité sont des outils très puissants pour caractériser et clarifier les modèles agronomiques que nous utilisons. Ce sont aussi des méthodes pertinentes lorsque l’on veut déployer un modèle à un niveau opérationnel, notamment parce que ces méthodes permettent de concentrer les efforts sur les paramètres vraiment importants du modèle et donc de faciliter son exploitation à plus large échelle. En voulant travailler avec des approches toujours plus précises (que ce soit à un niveau spatial ou temporel), il convient nécessairement de s’intéresser à la qualité des données que l’on utilise et donc, par voie de conséquence, à leur incertitude.
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

