A moins de sortir d’une période de cryogénisation ou d’avoir été enfermé dans un bunker pendant plusieurs années, il y a peu de chances que vous n’ayiez jamais entendus parler de réseau de neurones. En avoir entendu parler, c’est une chose. Comprendre ce à quoi à peut servir, c’en est une autre. Savoir comment ça marche, c’est une toute autre paire de manches. En regardant un peu ce qui se passe dans la littérature, dans les bouquins ou dans certains cours, on est très rapidement ensevelis sous les équations (sous les termes compliqués et j’en passe) sans même avoir vraiment compris de quoi on parle. J’avais envie d’apporter ici mon humble contribution pour essayer de démystifier et clarifier certains concepts.
Réseau de neurones, Deep learning et compagnie
Dans la famille « j’utilise des mots fourre-tout pour briller en société sans vraiment comprendre de quoi il s’agit », j’appelle l’« intelligence artificielle », le « machine learning », le « deep learning » et les « réseaux de neurones ». Alors, sans vraiment chercher à tout redéfinir (il y en a qui le feront bien mieux que moi) mais juste pour resituer un peu tout ce petit monde, il faut comprendre que le Deep Learning, c’est une branche du Machine Learning, qui est lui-même une branche de l’Intelligence Artificielle. Et quand on parle de réseau de neurones, on se réfère à un type d’algorithmes pour faire de l’apprentissage (le fameux Learning). Dans le domaine de l’agriculture, on peut par exemple apprendre à un modèle à faire de la prévision de rendement de blé, lui apprendre à identifier une adventice dans une parcelle, ou encore lui apprendre à reconnaitre une maladie sur une feuille de vigne. Pour faire cet apprentissage-là, on n’est pas obligés d’utiliser un réseau de neurones ! On peut utiliser plein de méthodes de Machine Learning différentes comme les arbres de décisions, les machines à vecteur de support (SVM), la régression logistique, l’analyse en composantes principales et j’en passe.
Il y a plusieurs types d’apprentissage différents, les principaux étant l’apprentissage supervisé, l’apprentissage non supervisé, et l’apprentissage par renforcement. On reviendra sur ces terminologies en fin d’article mais ce pour quoi on entend le plus parler de réseau de neurones, c’est l’apprentissage supervisé. En termes simples, on parle d’apprentissage supervisé parce que l’on va aider notre modèle à apprendre dans le sens où on a des données en entrée du modèle, et on connait les sorties auxquelles le modèle doit arriver. Si je reprends l’exemple de la prédiction de rendement de blé, j’ai accès à un certain nombre de données d’entrées du modèle (type de sol, données climatiques, pratiques agricoles…) et je connais le rendement obtenu avec ces données d’entrée, c’est-à-dire que je connais les sorties du modèle. Avec l’apprentissage supervisé, je demande à mon modèle d’apprendre à trouver le rendement sur une parcelle à partir des données d’entrée que je lui fournis. Et comme le rendement exact est connu, le modèle peut apprendre et s’améliorer. Encore une fois, ce qui vient d’être décrit – l’apprentissage supervisé – peut être mis au point avec d’autres méthodes que les réseaux de neurones !
Architecture du réseau de neurones
Pour rester en cohérence dans tout le reste de l’article, restons sur notre exemple de prédiction de rendement !
Commençons par l’architecture la plus simple du réseau de neurones : un réseau avec une seule couche d’un seul neurone (Figure. 1). Dans cet exemple très simple, on va utiliser 3 données en entrée :
- a_1 – la pluviométrie de l’année,
- a_2 – la température moyenne sur l’année, et
- a_3 – le type de sol (on va considérer que chaque type de sol a été labellisé par un numéro).
Ces données d’entrée servent à alimenter un modèle constitué d’un neurone de manière à produire une estimation de rendement (le petit chapeau sur le « y » est là pour préciser que ça reste une estimation). Pour commencer simplement, notre objectif est d’estimer si le rendement de l’année va être « fort » ou « faible ».
Propagation vers l’avant : Comment le rendement est-il estimé ?
Pour produire notre estimation de rendement, le neurone ici présent va réaliser une somme pondérée des données d’entrée à disposition. A chaque donnée d’entrée, le neurone va associer un poids (les w_1, w_2, w_3) et c’est la somme pondérée de ces poids avec les données d’entrée (\sum_{i=1}^{3} w_{i}a_{i} = w_{1}a_{1} + w_{2}a_{2} + w_{3}a_{3} ) qui va être utilisée pour estimer un rendement. Il faut comprendre ces poids comme une influence donnée à chaque donnée d’entrée. Si par exemple la pluviométrie est beaucoup plus importante que la température dans notre prédiction de rendement, le poids w_1 sera beaucoup plus grand que le poids w_2.
Dans notre exemple de prédiction binaire de rendement, on peut imaginer que si la somme pondérée des entrées \sum_{i=1}^{3} w_{i}a_{i} est supérieure à un seuil, alors le rendement sera « fort » (on peut parler de sortie ou d’output 1 en anglais) et que si elle est inférieure à ce même seuil, alors le rendement sera « faible » (on peut parler de sortie ou d’output 0 en anglais). On peut considérer que si notre prédiction a conduit à un rendement « fort », c’est en réalité que notre neurone a été activé (la somme pondérée est supérieure au seuil), alors qu’il est resté endormi ou désactivé (appelez-ça comme vous voulez) si notre prédiction a conduit à un rendement « faible ». Voyez ici un parallèle avec la façon dont fonctionne notre cerveau avec un certain nombre de neurones qui s’activent ou non pour donner des réactions toutes différentes les unes des autres (les flèches entre les entrées et le neurone peuvent être vues comme des synapses).
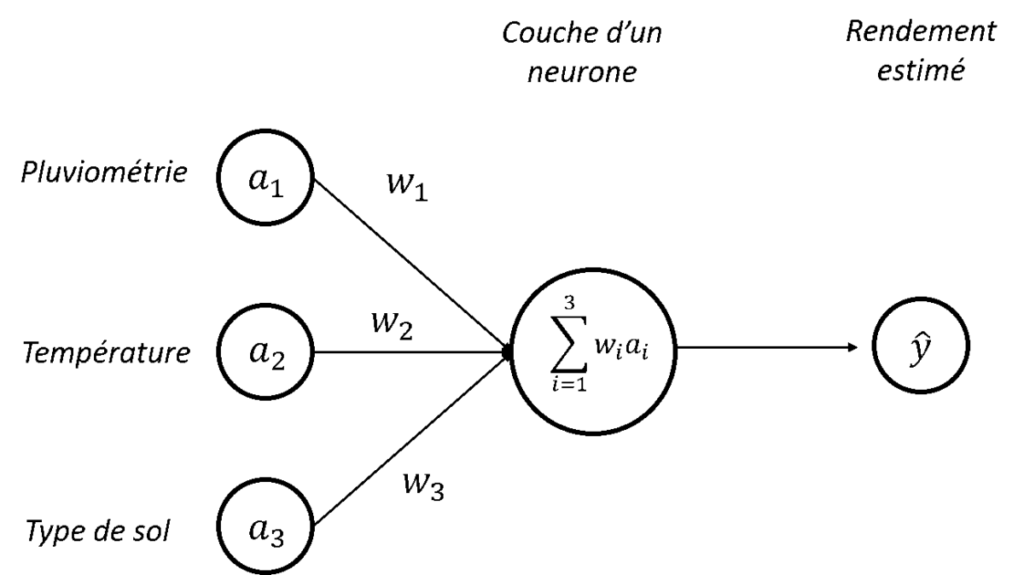
Figure 1 : Architecture d’un perceptron – Combinaison linéaire des entrées
Jusqu’ici, j’espère que tout le monde est encore à l’aise. On a en fait simplement réalisé une combinaison linéaire des entrées pour prédire un rendement faible/fort. Bon, si les neurones ne servaient qu’à ça, on n’en parlerait pas autant… L’architecture qui a été présentée ici (une couche d’un neurone) est appelée un perceptron. C’est la brique de base qui va être utilisée dans les réseaux de neurones.
Prêts pour la suite ? Rajoutons maintenant quelques notations :
Si nous reprenons l’idée de seuil dont nous avons parlé pour décrire si le neurone s’active ou non, notre petit cas d’étude peut s’écrire simplement avec les deux conditions suivantes :
Si \sum_{i=1}^{3} w_{i}a_{i} > Seuil, alors Output 1: Rendement “Fort”
Si \sum_{i=1}^{3} w_{i}a_{i} \le Seuil , alors Output 0: Rendement “Faible”
En réalité, ces deux inégalités ne nous arrangent pas beaucoup… et pour se simplifier un peu la vie (et pour beaucoup simplifier les notations plus tard !), on va utiliser un terme « b » connu sous le nom de biais du perceptron. Nos inégalités précédentes vont donc maintenant s’écrire comme ça :
Si \sum_{i=1}^{3} w_{i}a_{i} +b > 0, alors Output 1: Rendement “Fort”
Si \sum_{i=1}^{3} w_{i}a_{i} +b \le 0 , alors Output 0: Rendement “Faible”
On peut comprendre ce biais comme la facilité à activer un neurone. Si le biais est très fort, le neurone va être activé sans problème. A l’inverse, si le biais est très négatif, le neurone ne s’activera pas !
Pour simplifier encore les notations, nous allons appeler « z » notre terme à gauche de l’équation donc :
Si z > 0, alors Output 1: Rendement “Fort”
Si z \le 0 , alors Output 0: Rendement “Faible”
Reprenons notre perceptron avec ces nouvelles notations (Figure 2). Pour l’instant, ce qu’on a mis en place, c’est un modèle pour prédire un rendement fort/faible à partir d’une combinaison linéaire de pluviométrie, température et type de sol. Le problème, c’est que dans la majorité des cas, c’est quand même un peu plus compliqué que ça… Déjà, on peut avoir envie de prédire un rendement plus précis (avec une valeur numérique ou avec beaucoup plus de classes que simplement fort/faible). C’est un premier problème parce qu’avec l’architecture que l’on a actuellement, le modèle est seulement capable d’activer un neurone ou de ne pas l’activer donc on ne peut pas aller beaucoup plus loin que notre classification binaire (on peut par exemple avoir envie d’un neurone qui s’active à 40%). Et ensuite, on peut être relativement limité par le seul usage de relations linéaires entre nos variables d’entrée et notre sortie. Dans le domaine de l’agro-environnement, on fait quand même très souvent face à des phénomènes qu’on ne peut pas modéliser de façon linéaire. Mais alors, comment se sortir de toutes ces contraintes ? Avec la fonction d’activation pardi !
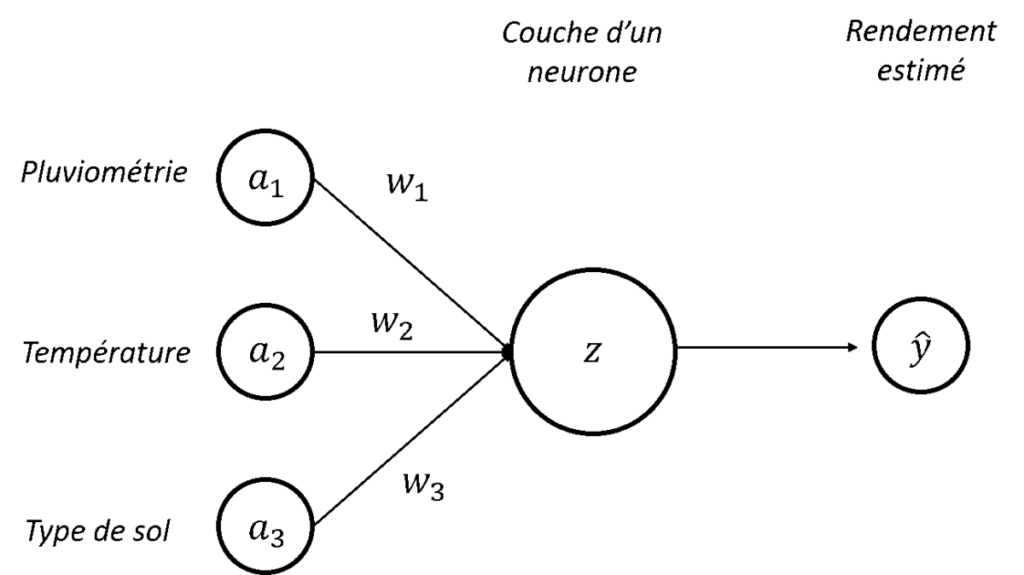
Figure 2. Architecture d’un perceptron – Nouvelles notations en place
La fonction d’activation, c’est la fonction que l’on va appliquer à un neurone pour décider si ce dernier va s’activer ou non. C’est une fonction que l’on va donc appliquer à notre entité z, et que l’on va noter \phi (Figure 3).
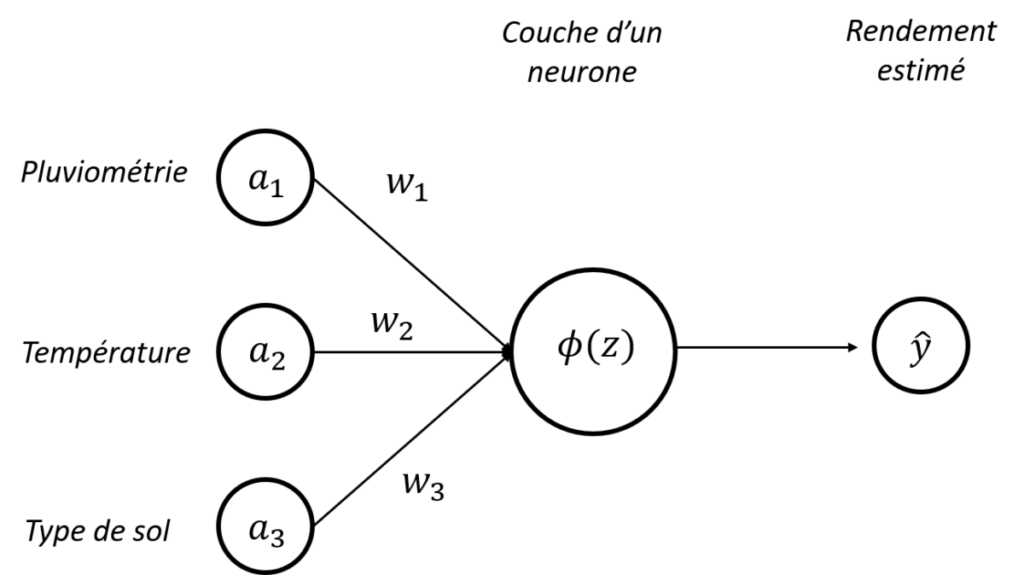
Figure 3. Architecture d’un perceptron – Activation d’un neurone
Et des fonctions d’activation, il en existe des tas ; chacune ayant ses spécificités. Je vais simplement vous en présenter trois mais gardez en tête qu’il en existe bien plus. La première, c’est la fonction d’activation « step » [Figure 4, gauche] et on peut voir que cette fonction ne retourne que deux valeurs sur tout son intervalle : 0 ou 1. C’est en fait tout simplement la fonction d’activation que l’on a utilisé jusqu’ici dans notre cas d’étude !
Pour aller un peu plus en profondeur sur l’activation des neurones, on peut aussi utiliser deux autres fonctions d’activation : la fonction « sigmoïde » (que l’on note plutôt \sigma et pas \phi), dont l’allure ressemble à un S [Figure 4, centre] et la fonction « ReLU » (que l’on note plutôt R et pas \phi). Notez que ces deux fonctions sont non linéaires !! Ce qui permet de s’affranchir des limites de la combinaison linéaire que l’on a vu précédemment. Concernant la fonction « sigmoïde », sur son intervalle de définition, on se rend déjà compte que la fonction peut retourner plus de valeurs que simplement 0 ou 1, ce qui laisse quand même plus de flexibilité sur l’activation ou non des neurones. La fonction sigmoïde est très plate pour des valeurs très faible ou très forte de notre variable « z ». Par contre, lorsque « z » prend des valeurs à peu près entre -2 et 2, la pente de la courbe devient très raide, ce qui signifie que de petits changements dans la valeur de « z » sont capables d’avoir une influence relativement forte sur la valeur de « z » et donc sur l’activation ou non des neurones.
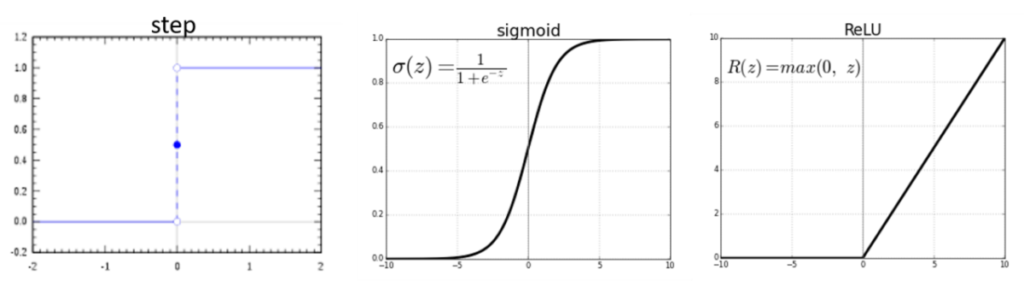
Figure 4. Exemples de trois fonctions d’activations différentes
Dans la pratique, la fonction « ReLu » est plus utilisée que la fonction « sigmoïde ».
Ce qui arrive dans ce paragraphe n’est pas fondamental pour comprendre le reste, c’est simplement pour les curieux (et vous pourrez y revenir à la fin de l’article, ce sera certainement plus clair) : Pour ceux que ça intéresse, la fonction « ReLu » est plus utilisée que la fonction « sigmoïde » parce que la fonction « sigmoïde » est sujette au phénomène que l’on appelle le problème de fuite de gradient (« vanishing descent problem » en anglais). Nous le reverrons un peu plus tard mais pour évaluer les poids w_1, w_2, w_3 de notre architecture de neurones, il faudra passer par une étape de backpropagation. Dans cette étape, l’objectif sera de minimiser une fonction de coût (qui n’est autre que l’erreur de notre modèle). Et pour minimiser cette fonction, il faudra calculer des gradients d’erreurs par rapport à ces poids (la fameuse descente de gradient), gradients qui vont devenir de plus en plus petits au fur et à mesure que l’on a beaucoup de couches et que l’on cherche à remonter vers les neurones des premières couches. A cause des extrémités plates de la fonction sigmoïde, on peut se retrouver « coincé » aux extrémités, avec des neurones qui ont du mal à apprendre, notamment les neurones des premières couches. Et ces neurones sont pourtant particulièrement importants parce que c’est eux qui vont extraire les grands patrons de nos données (et donc on a besoin qu’ils apprennent bien !).
Pour revenir à la fonction « ReLU », on observe une courbe plate pour des valeurs de « z » inférieures à 0 et une fonction linéaire pour des valeurs de « z » supérieures à 0. Attention, ça n’en fait donc pas une fonction linéaire sur la totalité de son intervalle, ça reste bien une fonction non linéaire !
Encore un petit point pour les curieux : On se libère donc en partie du phénomène de « vanishing descent problem » ici contrairement à la fonction « sigmoïde ». Il reste néanmoins quelques problèmes (moins importants), notamment le fait que les neurones pour lesquels les valeurs de « z » sont inférieures à 0 sont généralement considérés comme morts puisqu’ils ne pourront pas être réactivés (la pente est complètement plate donc les gradients calculés n’évolueront pas). Des alternatives existent, notamment le « Leaky ReLU » qui, au lieu d’avoir une courbe « plate » pour des valeurs de « z » inférieures à 0, a plutôt une droite linéaire avec une faible pente.
Et bien voilà, une fois qu’on a toute notre architecture (les données d’entrée, notre couche d’1 neurone, et notre fonction d’activation), on va pourvoir chercher à prédire notre rendement. Petit problème et non des moindres : Comment fixer les poids w_1, w_2, w_3 ? En gros la question, c’est comment notre modèle apprend ??? C’est la backpropagation
Propagation vers l’arrière [Backpropagation] : Comment le modèle apprend-t-il?
Si on est toujours sur la même longueur d’onde, on veut utiliser nos trois données d’entrées (pluviométrie, température, type de sol) pour prédire si le rendement de l’année sera « faible » ou « fort ». Pour construire et évaluer un modèle de prédiction, ce qui se fait classiquement est de séparer son jeu de données en un jeu d’apprentissage, et un jeu de validation. Le modèle « apprend » sur le jeu d’apprentissage, puis le modèle est validé sur le jeu de validation. On va donc ici se concentrer sur un jeu d’apprentissage, c’est-à-dire un jeu pour lequel les entrées et les sorties sont connues. On a donc un jeu de données d’apprentissage que l’on peut voir comme un tableau avec, en lignes les différents sites d’étude, et en colonnes, les valeurs de pluviométrie, température, type de sol, et rendement obtenu (faible ou fort).
Comme on l’a vu sur la figure 3 dans notre cas d’étude simplifié, le rendement que l’on prédit avec notre modèle s’écrit \phi(z). On peut considérer que notre modèle est bon s’il est capable de trouver la bonne valeur de sortie « y » (le rendement vrai) associé aux données d’entrées correspondantes. On peut donc construire une fonction d’erreur simple (qu’on peut aussi appeler coût du modèle) C_{x} pour chacun des sites d’études x.
C_{x} = [\phi(z(x)) -y(x)]^2
Sur cette fonction de coût, on pénalise (avec le carré) les sites pour lesquels le rendement a été mal prédit. L’objectif, sans trop de surprise, est de chercher à minimiser cette fonction de coût, ce qui revient à dire que l’on cherche à minimiser les erreurs de prédiction sur les sites d’étude. A partir de cette fonction de coût par site d’étude, on peut construire une fonction de coût pour l’ensemble du modèle qui est la moyenne du coût associé à chaque site d’étude
C = \frac{1}{n} \sum C_{x}
Avec n le nombre de sites d’études
Il faut bien comprendre que cette fonction de coût dit simplement au modèle s’il a bien fait ou non son travail de prédiction. Mais il ne lui dit pas comment s’améliorer… En fait, ce qu’on cherche vraiment à faire, c’est trouver les meilleurs poids à l’entrée du modèle (nos w_1, w_2, w_3 et sans oublier le biais du neurone b !) pour que le modèle prédise le mieux possible. Au tout départ, les poids sont donnés de manière aléatoires (nous y reviendrons plus tard) mais au fur et à mesure que le modèle apprend, il faut lui faire comprendre dans quel sens le modèle doit faire bouger ses poids et le biais pour mieux prédire. Et pour ça, quoi de mieux qu’utiliser des dérivées !! Et bien oui, ce qu’on veut calculer, c’est la dérivée de la fonction coût par rapport à w_1 pour savoir comment changer w_1 pour minimiser l’erreur ou le coût du modèle, et idem pour w_2, w_3 et b .
Allez, c’est parti, on s’y lance au moins pour w_1 (et ce sera la même chose pour w_2, w_3 et quasiment la même chose pour b) ! Un tout petit peu de maths, ça fait pas mal de mal. On va donc calculer la dérivée de notre fonction de coût par rapport à w_1, que l’on va noter \frac {\partial C_{x}}{\partial w_{1}}. On va pouvoir calculer cette dérivée comme suit :
\frac {\partial C_{x}}{\partial w_{1}} = \frac {\partial z(x)}{\partial w_{1}} \times \frac {\partial C_{x}}{\partial z(x)}
On rappelle les formules de z et de C_{x} que l’on va utiliser :
z(x)=w_{1}a_{1}(x) + w_{2}a_{2}(x) + w_{3}a_{3}(x) + b(x)
C_{x} = [\phi(z(x)) -y(x)]^2
On va calculer une variation de la fonction de coût par rapport à w_1 pour chaque site d’étude et c’est ensuite la moyenne de toutes ces variations qu’on va appliquer à w_1 comme on va le voir après. Maintenant, dérivons les formules de z(x) et de C_{x} précédentes de manière à calculer \frac {\partial z(x)}{\partial w_{1}} et \frac {\partial C_{x}}{\partial z(x)}.
\frac {\partial z(x)}{\partial w_{1}} = a_{1}(x)
\frac {\partial C_{x}}{\partial z(x)} = 2 \times [\phi(z(x)) -y(x)] \times \phi'(z(x))
Grâce à ces formules, on sait dans quel sens faire varier le poids w_1 pour améliorer notre modèle ! Je rappelle qu’on a calculé la variation de la fonction coût par rapport à w_1 pour un site d’étude x et que c’est bien la moyenne de variation sur tous les sites d’étude qui nous intéresse pour savoir comment faire varier w_1
\frac {\partial C}{\partial w_{1}} = \frac {1}{n} \sum_{x} \frac {\partial C_{x}}{\partial w_{1}}
On fait ensuite varier w_1 en utilisant la formule suivante :
w_{1} = w_{1} - \eta \times \frac {\partial C}{\partial w_{1}}
Avec \eta la vitesse d’apprentissage (ou learning rate en anglais) que l’utilisateur fixe comme hyperparamètre du modèle (on reviendra sur cette notion d’hyperparamètre). Vous pourrez parfois voir le learning rate noté aussi \alpha. On peut voir un peu le terme \eta comme la vitesse avec laquelle les poids et biais vont converger vers leur valeur optimale, et donc la fonction de coût va converger vers sa valeur minimale. Mais on a qu’à prendre une valeur de \eta super grande alors !? Non…. Le problème, c’est que si vous utilisez une valeur de \eta trop grande, l’algorithme risque de diverger au lieu de converger ! On peut se dire que les poids et biais essayent de converger tellement vite qu’ils ratent leur valeur optimale et vont se perdre complètement… Si on prend une valeur de \eta faible, l’algorithme va converger trop lentement, ce qui n’est pas forcément grave, sauf si la fonction de coût se retrouve bloquée dans un minimum local, et donc n’atteint pas sont minimum global, c’est-à-dire son optimum. Il faut donc ne pas choisir n’importe quoi comme valeur de \eta. On peut trouver des valeurs dans la littérature ou sur des modèles existants qui ne fonctionnent pas trop mal. C’est après à l’utilisateur de retravailler son paramétrage. Je n’ai pas clairement mentionné ce que l’on a vu jusqu’ici mais en fait, on vient de parler de la descente de gradient (« gradient descent ») qui fait souvent peur ! La descente de gradient, ce n’est en fait rien d’autre que le terme « - \eta \times \frac {\partial C}{\partial w_{1}} ». Il y a un signe négatif parce qu’on cherche la direction pour diminuer la fonction de coût et on parle de gradient avec la dérivée de la fonction de coût par rapport à w_1. L’hyperparamètre \eta permet de rajouter une notion de proportionnalité.
Note : vous pourrez voir \frac {\partial C}{\partial w_{1}} noté de façon plus simple dw_{1} :
w_{1} = w_{1} - \eta \times dw_{1}
Il suffit alors de refaire la même chose pour actualiser les valeurs de w_2, w_3 et b (on ne le fait pas ici mais c’est le même principe).
Si on résume rapidement ce qui se passe avec les réseaux de neurones, en fait :
- On initialise les poids du réseau (on y reviendra plus tard mais il faut bien partir de poids existants au départ avant de les changer)
- Pour chaque site d’étude x
- On fait une prédiction (c’est la propagation vers l’avant)
- On calcule le coût de la prédiction associé au site x
- On calcule la dérivée de la fonction de coût par rapport aux poids et biais du modèle (c’est la back propagation)
- On moyenne les résultats sur l’ensemble du jeu de données et on actualise les poids/biais du réseau
Extension aux réseaux de neurones multicouches
L’exemple précédent est relativement simple, on ne va pas se le cacher, mais il a permis (je l’espère) de clarifier un certain nombre de notions. Dans l’architecture du perceptron que l’on a vue, il n’y a effectivement qu’une seule couche composée d’un seul neurone. Pour les tâches complexes que chacun est susceptible d’avoir à réaliser, cette architecture n’est pas suffisante. Il va en effet falloir rajouter des couches et des neurones par couche mais pas d’inquiétude, la totalité des concepts que l’on a vu reste d’actualité ; on va seulement rajouter quelques notations pour que toutes nos équations précédentes puissent être étendues au cas des réseaux de neurones multicouches ou « profonds ». On parle de profondeur lorsque l’on rajoute des couches dans le réseau de neurones, pour permettre au modèle de découvrir et d’apprendre des relations de plus en plus complexes. Le perceptron est un réseau simple puisqu’il n’y a pas qu’une seule couche (on peut parler de « shallow » learning pour se différencier du « deep » learning). Voyons ci-dessous une architecture un peu plus compliquée :
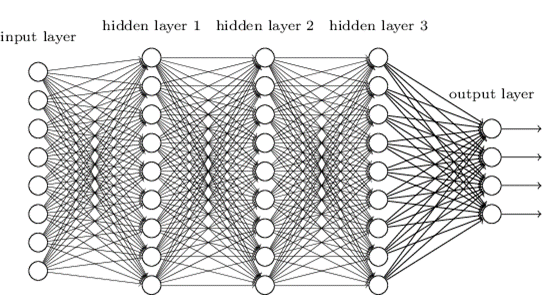
Figure 5. Architecture d’un perceptron multi-couches
On peut voir ici une couche avec les données d’entrée (input layer), trois couches que l’on dit cachées parce qu’elles font le lien entre les entrées et les sorties (hidden layers 1, 2 et 3), et la couche de sortie (output layer). Dans cet exemple, chaque couche cachée est composée d’autant de neurones mais ce n’est pas nécessairement le cas ! On voit également plusieurs couches de sortie, ce qui peut apparaitre contre intuitif au départ. Mais imaginez que vous vouliez prédire quatre classes de rendement (Très faible, Faible, Fort, Très fort), vous aurez alors besoin de quatre sorties avec pour chacune, la probabilité d’appartenir à chacune des classes.
Avec cette nouvelle architecture, vous pouvez commencer à sentir que l’on va devoir manipuler beaucoup de données d’entrée, beaucoup de poids (chaque trait sur la figure représente un poids) et beaucoup de biais (un par neurone). Il faut donc clarifier quelques notations ! Dans l’architecture du perceptron, nous avons appelé a_1, a_2, a_3 les données d’entrée de notre modèle, w_1, w_2, w_3 les poids associés aux trois données d’entrée utilisées, b le biais du neurone de notre modèle et z la somme du biais et de la somme pondérée des entrées \sum_{i=1}^{3} w_{i}a_{i}+b . Rien de compliqué mais regardez maintenant les nouvelles notations :
- w^{l}_{jk} est le poids de la connexion entre le neurone k de la couche l-1 et le neurone j de la couche l
- b^{l}_{j} est le biais du neurone j de la couche l
- a^{l}_{j} est l’activation du neurone j de la couche l 1\phi(z)[/latex]].
- La couche de donnée d’entrée est la couche 0 et en général on ne la compte pas quand on compte le nombre de couches totales dans l’architecture de neurones
- L est le nombre de couches dans le réseau de neurones donc aussi le numéro de la dernière couche (encore une fois on ne compte pas la première)
Avec un schéma, ce sera encore plus clair (un petit peu plus petit que le précédent pour y voir quelque chose).
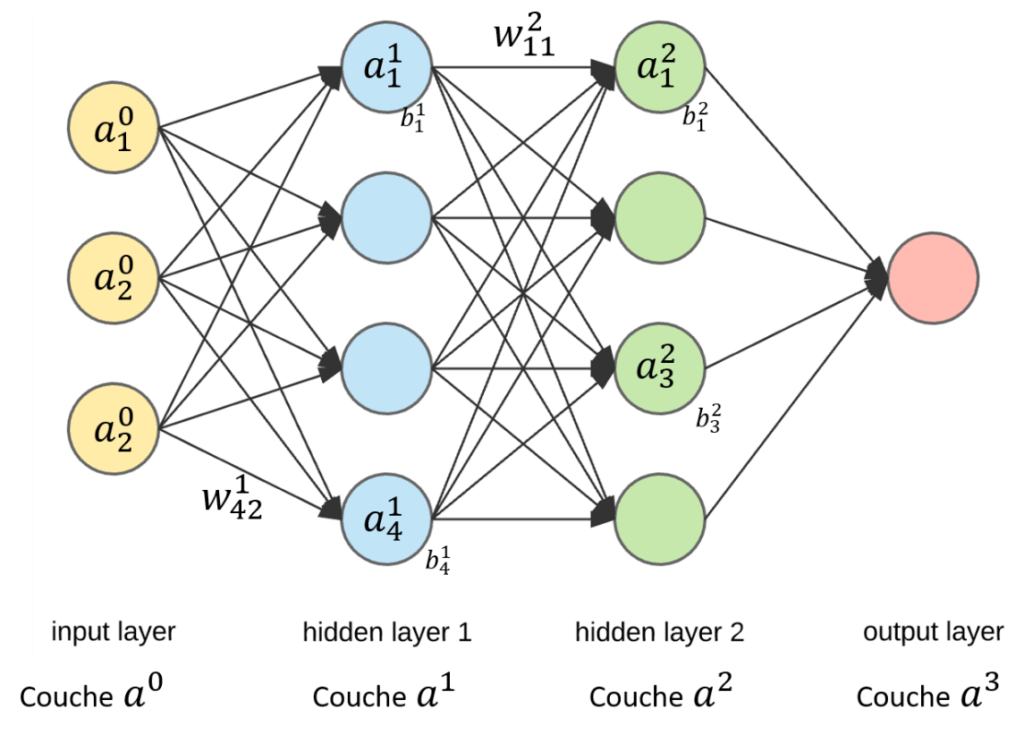
Figure 6. Architecture d'un perceptron multi-couches avec les nouvelles notations. Il y a ici L = 3 couches
Avec ces nouvelles notations, on se rend compte qu’on va pouvoir facilement relier l’activation d’un neurone sur une couche avec l’activation d’un neurone qui lui est lié sur une couche précédente :
a^{l}_{j} = \phi (\sum_{k} w^{l}_{jk}a^{l-1}_{j}+b^{l}_{j})
On voit bien le parallèle avec nos anciennes notations :
\phi(z) = \phi (\sum_{i=1}^{3} w_{i}a_{i} +b)
Et si, pour simplifier encore les notations, on écrit l’équation précédente sous une forme matricielle
a^{l} = \phi (w^{l}a^{l-1}+b^{l}) = \phi(z^{l})
Et voilà, on a généralisé notre architecture à un réseau de neurones multi-couches ! On ne va quand même pas s’arrêter là ! On peut utiliser ces notations pour étendre aussi la fonction de coût et la backpropagation à un réseau multicouches :
C_{x} = [a^{L}(x) -y(x)]^2
Ici, c’est bien l’indice L qu’on utilise puisque c’est l’indice de la dernière couche du réseau de neurone, c’est-à-dire la couche de sortie et c’est bien celle là que l’on doit comparer à la valeur vraie de rendement y(x) correspondant au site d’étude x. De la même façon, la fonction de coût pour l’ensemble du modèle (et pas seulement un site d’étude) s’écrit :
C = \frac{1}{n} \sum C_{x}
Avec n le nombre de sites d’études
Pour la backpropagation, on cherche à nouveau à évaluer la dérivée de la fontion coût par rapport à tous les poids fixés dans le modèle (et aussi par rapport aux biais des neurones, on ne les oublie pas !):
\frac {\partial C_{x}}{\partial w^{l}} = \frac {\partial z^{l}(x)}{\partial w^{l}} \times \frac {\partial a^{l}}{\partial z^{l}(x)} \times \frac {\partial C_{x}}{\partial a^{l}}
\frac {\partial C_{x}}{\partial b^{l}} = \frac {\partial z^{l}(x)}{\partial b^{l}} \times \frac {\partial a^{l}}{\partial z^{l}(x)} \times \frac {\partial C_{x}}{\partial a^{l}}
Notez bien qu’ici, par rapport à la première architecture simple qu’on a utilisé, on a rajouté les termes d’activation a^{l}. S’en suit alors le même travail de dérivation que précédemment (avec les formules actualisées bien évidemment) que je ne détaillerai pas ici. Ces calculs vous permettent encore une fois de trouver dans quel sens faire varier les poids de votre modèle pour l’améliorer. On moyenne les variations sur l’ensemble des sites d’étude :
\frac {\partial C}{\partial w^{l}} = \frac {1}{n} \sum_{x} \frac {\partial C_{x}}{\partial w^{l}}
\frac {\partial C}{\partial b^{l}} = \frac {1}{n} \sum_{x} \frac {\partial C_{x}}{\partial b^{l}}
On actualise ensuite les poids et les biais :
w^{l} = w^{l} - \eta \times \frac {\partial C}{\partial w^{l}}
b^{l} = b^{l} - \eta \times \frac {\partial C}{\partial b^{l}}
Quelques références à regarder !
- Un ensemble de quelques vidéos avec de très belles illustrations : https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw
- Un bouquin en ligne très détaillé sur les réseaux de neurones : http://neuralnetworksanddeeplearning.com/
- Une étude de la Chaire AgroTIC sur le deep learning et ses usages en agriculture : https://www.agrotic.org/wp-content/uploads/2018/12/2018_ChaireAgroTIC_DeepLearning_VD2.pdf
- Quelques sites webs avec des animations/informations pertinentes :
Soutenez les articles de blog d'Aspexit sur TIPEEE
Un p'tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?


1 commentaire sur « Réseau de neurones – On va essayer de démystifier un peu tout ça (1) – Architecture neuronale »