De manière générale, lorsque l’on veut évaluer la robustesse et/ou la généralité d’un algorithme, on a besoin de le tester sur un grand nombre de données, avec des caractéristiques assez variées, pour s’assurer que l’algorithme va donner des résultats concluants dans la grande majorité des cas. Si on avait les moyens d’avoir des données réelles ou des données de terrain en assez grande quantité, on pourrait se permettre de tester l’algorithme sur ces données-là. Malheureusement, pour des raisons assez évidentes de coût, de temps ou de difficulté d’acquisition, on a assez peu accès à des sources conséquentes de données réelles. Pour pallier ce problème, on peut travailler avec des données théoriques en faisant de la simulation, en s’assurant au préalable que les données simulées ressemblent le plus possibles aux données réelles (sinon, il y aurait assez peu d’intérêt à la simulation…).
En Agriculture de Précision, les données spatialisées présentent des structures de corrélation, notamment spatiales (mais pas que), qu’il faut donc recréer lorsque l’on fait de la simulation. Dans un précédent post, nous avons vu comment simuler une variable agronomique spatialisée sur une parcelle avec une structure spatiale donnée. Dans ce post, nous allons voir comment simuler deux variables agronomiques spatialisées sur la même parcelle, ces deux variables étant corrélées entre elles. Ce post a été rédigé à partir de l’article de Baptiste Oger [« Combining target sampling with within field route-optimization to optimise on field yield estimation in viticulture »] soumis dans le journal « Precision Agriculture » en 2020. L’article s’intéresse au développement d’une nouvelle méthode d’optimisation de l’échantillonnage pour mieux estimer le rendement d’une parcelle de vigne (les lecteurs intéressés peuvent aller y jeter un coup d’œil – ça y parle d’optimisation sous contraintes mais ce n’est pas directement le sujet de ce post). Dans le cadre de ce travail, les auteurs font l’hypothèse que, sous certaines conditions pédo-climatiques, le rendement de la culture est corrélé à un indicateur de végétation (NDVI) de la culture. En utilisant cette information de végétation comme information auxiliaire (plus facilement accessible que le rendement) pour choisir des points d’échantillonnage d’intérêt, il serait alors possible de faciliter et améliorer l’estimation du rendement dans la parcelle. Pour tester la pertinence de leur méthode d’échantillonnage, un des pré-requis de cet article était donc de pouvoir générer des données simulées de rendement et de NDVI, plus ou moins corrélées entre elles….
Présentation de la méthode de génération de données spatiales cross-corrélées
L’idée générale derrière la méthode est relativement simple. La première étape consiste à créer une variable spatialisée G sur une parcelle donnée (de la même façon que ce qui avait été présenté dans un précédent post) sauf que l’on crée ici cette variable sans aucun effet pépite. Les données de cette variable ne sont donc pas bruitées du tout, l’ensemble de la variabilité est structuré dans l’espace (si on devait représenter la structure spatiale à l’aide d’un variogramme, le variogramme passerait par l’origine (0,0) du graphique). A partir de cette variable spatialisée G, qui est utilisée comme référence, deux variables agronomiques – V1 et V2 – vont être créées. En reprenant le cas d’étude de l’article de Baptiste, V1 peut être assimilée à la couche de rendement et V2 à la couche de NDVI. Une couche de bruit (E_{V1}) sera rajoutée sur G pour construire V1, et une couche de bruit différente (E_{V2}) sera rajoutée sur G pour construire V2. Le bruit rajouté à G est aléatoire, il n’a aucune structure spatiale. C’est un pur effet pépite en quelque sorte. En fonction des caractéristiques de la variable G de départ, et du bruit qui va être rajouté, on va pouvoir jouer sur trois critères :
- La distance d’auto-corrélation spatiale de G, V1 et V2 (c’est la portée du variogramme),
- La proportion de bruit dans les données de V1 (on ne peut pas contrôler en même temps celle de V1 et de V2 donc on fixe celle de V1 d’abord, et on peut travailler sur celle de V2 en fonction de ce qu’on a fait pour V1).
- Le degré de corrélation entre les variables V1 et V2
On va maintenant représenter quelques équations pour rentrer un tout petit peu plus dans le détail de cette méthode. Promis, rien de trop compliqué ! La Figure 1 ci-dessous vous permettra de mieux appréhender la méthode avant de vous lancer dans la partie théorique.
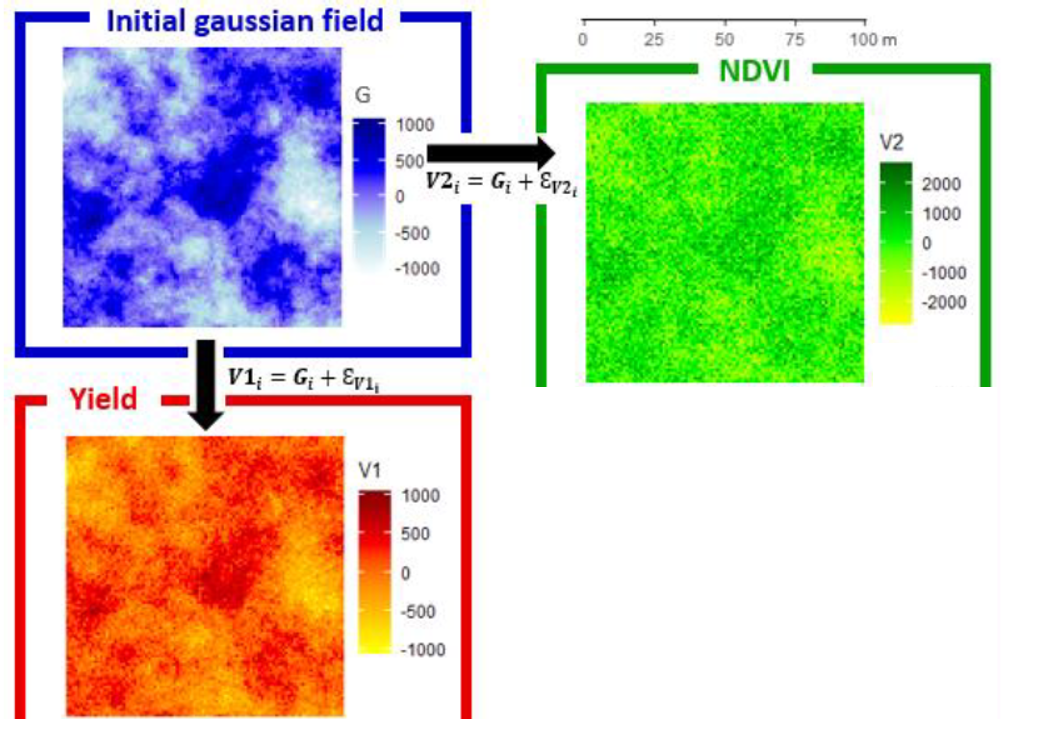
Figure 1. Génération de deux variables spatialisées corrélées entre elles
Théorie de la méthode
On va commencer par définir quelques notations :
- G est une variable régionalisée sans aucun effet pépite
- E_{V1} est la variable de bruit qui sera ajoutée à G pour construire V1. E_{V1} est une variable avec une distribution gaussienne centrée sur 0 avec une variance \sigma^2_{EV1}
- E_{V2} est la variable de bruit qui sera ajoutée à G pour construire V2. E_{V2} est une variable avec une distribution gaussienne centrée sur 0 avec une variance \sigma^2_{EV2}
- Nous allons construire les variables G, E_{V1}, E_{V2}, V1 et V2 sur une grille de 100m x 100 m, avec des pixels de 1 mètre de côté. Il y aura donc 10000 données pour chaque variable. On rajoute la notation concernant l’indice « i » pour caractériser la « ième » donnée. On peut donc définir G_i, E_{V1i}, E_{V2i}, V1_i ou encore V2_i
Pour construire G, on a vu comment le faire avec R dans un précédent post. On peut en effet simuler un champ gaussien en renseignant les paramètres variographiques que l’on souhaite (pépite, portée, variance totale). Ici, l’effet pépite est mis à 0 parce que je vous rappelle que l’on souhaite générer une variable régionalisée sans aucun effet pépite. La portée du variogramme qui sera définie pour G sera indirectement celle que l’on aura pour V1 et V2 (l’ajout des bruits E_{V1} et E_{V2} ne jouera pas sur la portée des variogrammes de V1 et V2).
En suivant ce qui a été défini précédemment, on définit simplement les variables V1 et V2 en chaque point « i » comme suit :
V1_i=G_{i}+E_{V1i} with E_{V1i} \sim N(0,\sigma^2_{EV1})
V1_i=G_{i}+E_{V2i} with E_{V2i}\sim N(0,\sigma^2_{EV2})
Puisque les variables de bruit E_{V1} et E_{V2} suivent une distribution gaussienne centrée sur 0, les seuls paramètres sur lequels il est possible de jouer pour influer sur les critères la proportion de bruit dans les données de V1 ou sur le degré de corrélation entre V1 et V2, ce sont les variances \sigma^2_{EV1} et \sigma^2_{EV2} des variables E_{V1} et E_{V2}
Travaillons d’abord sur La proportion de bruit dans l’espace pour V1
Soit C_{1} la proportion de variance structurée dans l’espace pour V1
C_{1} = \frac{effet pépite de V1}{ variance totale de V1}
Comme la variable G de référence est une variable sans effet pépite, l’effet pépite de V1 est simplement la variance de E_{V1}. La variance totale de V1 est la somme de celle de G et E_{V1}
C_{1}= \frac{\sigma^2_{EV1}}{\sigma^2_{G}+\sigma^2_{EV1}}
En isolant \sigma^2_{EV1} sur la gauche de l’équation,
\sigma^2_{EV1} = \frac{C_{1} \times \sigma^2_{G}}{1-C_{1}}
On peut donc jouer sur la proportion de bruit dans V1 en variant la valeur de C_{1}, pour une variance totale de G fixée.
Travaillons ensuite sur La corrélation entre V1 et V2
Intéressons nous à la covariance entre les variables V1 et V2 avant d’aller regarder ce qui se passe sur le degré de corrélation entre V1 et V2. La covariance s’écrit simplement :
Cov(V1,V2)=Cov(G+E_{V1},G+E_{V2})
En décomposant l’équation précédente avec la formule de la covariance, on obtient:
Cov(V1,V2)=Cov(G,G)+Cov(G,E_{V1})+Cov(G,E_{V2})+Cov(E_{V1},E_{V2})
Les variables G, EV1, et EV2 sont toutes les trois des variables aléatoires. Chacune est en plus indépendante l’une de l’autre. La théorie nous dit que la covariance de deux variables aléatoires indépendantes est nulle. L’équation précédente peut donc se simplifier :
Cov(V1,V2)=Cov(G,G)=Var(G)=\sigma^2_{G}
Nous venons de décomposer la formule de la covariance – Cov(V1,V2) – mais ce qui nous intéresse, c’est bien de pouvoir choisir la corrélation entre les variables V1 et V2 – Cor(V1,V2). Les covariances et corrélations entre V1 et V2 sont reliées par la formule de Pearson :
Cor(V1,V2)=\frac{Cov(V1,V2)}{\sqrt{Var(V1)} \times \sqrt{Var(V2)}}
En remplaçant les termes de l’équation,
Cor(V1,V2)=\frac{\sigma^2_{G}}{\sqrt{\sigma^2_{G}+\sigma^2_{EV1}} \times \sqrt{\sigma^2_{G}+\sigma^2_{EV2}}}
Enfin, en réorganisant l’équation, on est capable de définir comment régler le bruit de la variable V2 en fonction du degré de corrélation entre V1 et V2:
\sigma^2_{EV2}=(\frac{\sigma^2_{G}}{\sqrt{\sigma^2_{G}+\sigma^2_{EV1}} \times Cor(V1,V2)})^2-\sigma^2_{G}
Et voilà ! Ce que nous montre les équations précédentes, c’est qu’on sait comment régler les variables bruit E_{V1} et E_{V2} pour avoir la proportion de bruit dans l’espace pour V1, et le degré de corrélation entre V1 et V2 voulus. Par exemple, si je fixe une proportion de bruit de 0.3 pour V1, et que je veux que la corrélation entre V1 et V2 soit de 0.7 ; je peux calculer \sigma^2_{EV1} et \sigma^2_{EV2} en conséquence et avoir les variables V1 et V2 attendues.
Quelques petits plus
Pour aller un peu plus loin dans la simulation de données, deux options sont envisagées dans l’article de Baptiste Oger. Rassurez-vous, c’est plus simple que ce qui a été présenté au-dessus. Ces options sont présentées sur la figure 2.
La première est de ré-échelonner les valeurs des données des variables V1 et V2. Typiquement, une valeur de rendement négative n’a pas beaucoup de sens. De la même façon, les valeurs de végétation de NDVI sont plutôt comprises entre 0 et 1. Pour représenter plus fidèlement les variables de rendement et de NDVI, il est par exemple possible de transformer linéairement les données de V1 et V2, en fixant la valeur moyenne des variables de rendement (Y) et de NDVI attendues, ainsi que leur niveau de variance.
Y_{i}= \bar{Y} + V1_{i}
NDVI_{i}= \bar{NDVI} + V2_{i} \times \alpha
Avec \bar{Y} et \bar{NDVI}, les rendement et NDVI moyens attendus
Ces transformations n’affectent en aucun cas le paramétrage que nous avons vu plus haut, à savoir la portée du variogramme de G, V1 et V2 ; la proportion de bruit de V1, ou encore la corrélation entre V1 et V2.
La deuxième option est de modéliser des phénomènes un peu spécifiques dans la parcelle – zones de maladies localisées, groupe de pieds manquants à certains endroits de la parcelle – pour avoir une meilleure représentation de la réalité. Notez que zones seront ajoutées sur la variable V2 (NDVI) pour complexifier les structures de corrélation entre V1 et V2. Ces phénomènes assez localisés dans les parcelles sont assez difficilement modélisables par un simple ajout de bruit aléatoire comme ce qu’on a fait avec E_{V1} et E_{V2}. Ca pourrait arriver, certes, mais il faudrait que, de façon aléatoire, plusieurs bruits sur des données proches soient très forts ou très faibles (ce qui n’arrivera pas tous les quatre matins…). Baptiste propose plutôt de sélectionner un petit nombre de données voisines pour constituer une zone, et d’affecter une même valeur à toutes les données de cette zone, cette valeur étant soit anormalement haute, soit anormalement basse par rapport à la moyenne attendue de NDVI. Un filtre assez simple pourra être utilisé pour lisser les données autour de cette zone pour ne pas avoir de changements de valeurs trop brusques entre l’intérieur et l’extérieur d’une zone (on observe d’ailleurs dans la réalité plutôt des gradients de données dans les parcelles que des changements très brusques). Ce processus pourra être répété pour autant de zones que l’on voudra faire apparaitre sur la parcelle.
Avec ce post et un des posts précédents, vous êtes maintenant capables de simuler une variable auto-corrélée dans l’espace, mais aussi deux variables corrélées entre elles dans l’espace !
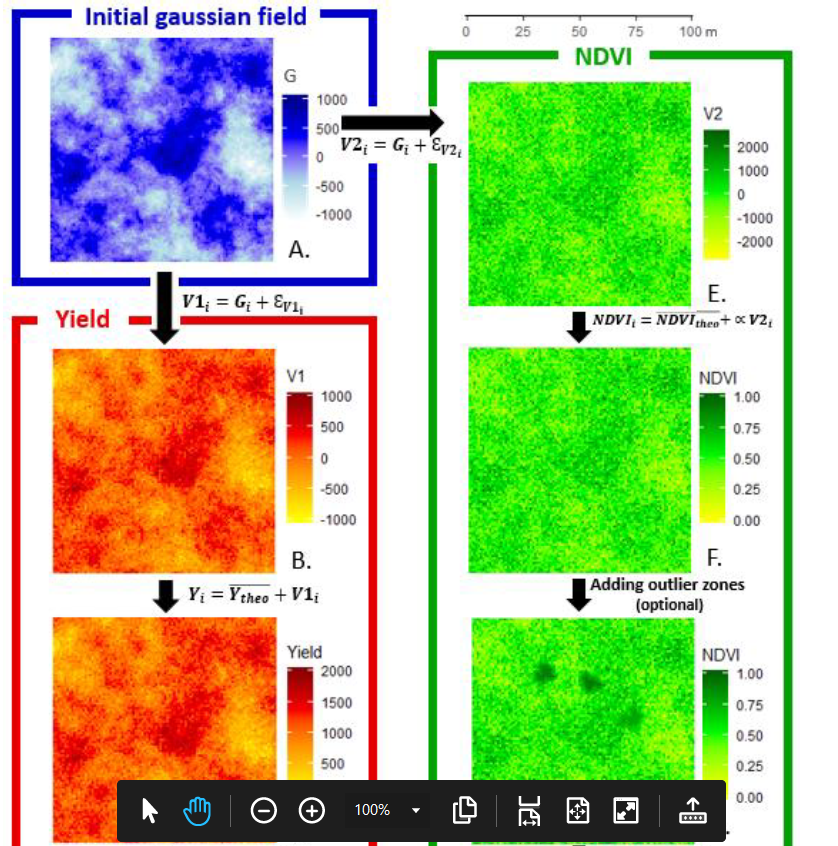
Figure 2. Génération de deux variables spatialisées corrélées entre elles – affinage des variables
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

