S’il y a bien un sujet délaissé quand on travaille avec des données spatialisées, c’est celui du système de coordonnées de référence. En général, on essaie de passer le moins de temps possible sur le sujet – souvent parce que ce n’est pas très clair – et on assume qu’on a collecté nos données dans un super système de coordonnées ou que notre fournisseur/prestataire a fait le travail pour nous (sinon, c’est sa faute !). Malgré tout, il arrive que l’on ne se souvienne plus du système de coordonnées utilisé lors de la collecte de données, ou que l’on reçoive des données tout simplement sans système de coordonnées associé. Rajoutons à cela par exemple la projection à la volée dans QGIS qui nous donne l’impression que nous couches sont bien localisées (après tout, QGIS arrive à les ouvrir !). Ensuite viennent la manipulation, géo-traitements en tout genre, et l’analyse de ces données. Et là, les ennuis commencent parce qu’on se rend compte que c’est quand même bien le bordel dans la projection des couches.
Être au clair sur les systèmes de coordonnées avant la gestion d’un projet à base de données spatialisées, ça permet d’éviter bien des problèmes !
Le Géoide
Pour pouvoir localiser des observations sur la Terre, il faut commencer par savoir à quoi ressemble la Terre et en avoir une représentation, sinon on aura assez peu de chances de localiser quoi que ce soit dessus. Vous avez peut-être déjà entendu parler du géoide, cette forme cabossée, difforme et pas très sexy de la Terre (Figure 1).
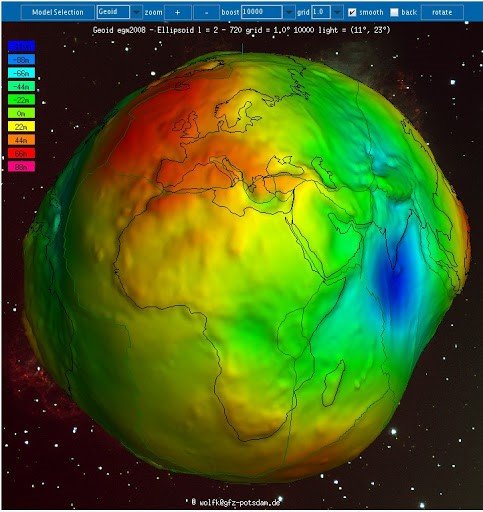
Figure 1. Géoide : surface équipotentielle de référence du champ de gravité terrestre
Le géoide, c’est la forme qu’aurait la surface de l’océan sous la seule influence de la gravité et de la rotation de la Terre. Et c’est cette forme cabossée qu’on devrait voir par satellite s’il n’y avait pas de phénomènes de marée et de vent (sur la figure 1, les variations sont un peu exacerbées, on ne devrait pas voir de creux aussi profond, mais ça permet de mieux comprendre ce qui se passe). Le géoide, c’est l’une des surfaces que l’on considère comme référence de l’altitude coincidant avec le niveau moyen des mers. Quand on dit par exemple que le sommet de telle colline est à 130 mètres d’altitude par rapport au niveau de la mer, on considère en réalité que c’est 130 mètres par rapport au géoide (ou à une autre surface, si on ne prend pas le géoide comme référence).
Les Ellipsoides
Malgré le fait que le géoide est une très bonne représentation de la terre, quand on veut commencer à modéliser la Terre avec des équations mathématiques, ça devient très compliqué parce qu’il y a quand même beaucoup de bosses et de creux, donc bon courage même si vous êtes super calés en maths. Pour limiter ce problème, une des actions entreprise a été d’approximer le géoide par des ellipsoides (Figure 2) puisqu’en tant que bons mathématiciens, on est capables de bien caractériser les formes des ellipsoides (longueurs de l’axe principale, et demi grand-axe ; je vous laisse vous replonger dans vos anciens cours de maths !). On aurait pu aussi représenter le géoide par un cercle (l’équation d’un cercle est encore plus simple !) mais la Terre a tendance à être aplatie aux pôles, ce qui a plutôt orienté vers l’utilisation des ellipsoides.
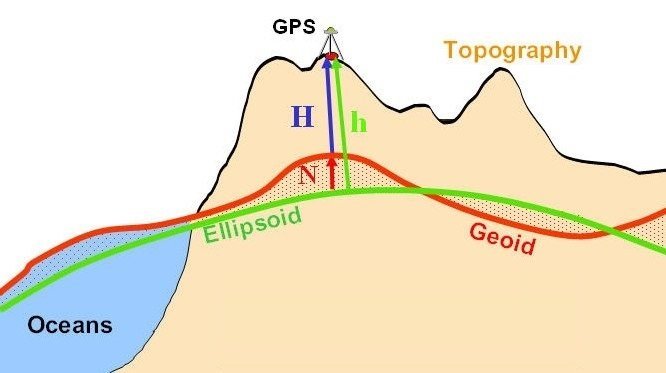
Figure 2. Approximation du géoide par une ellipsoide
Lorsque l’on choisit une ellipsoide particulière pour approximer le géoide, on dit que l’on choisit une ellipsoide « de référence », tout simplement parce que les coordonnées de nos observations seront déterminées en fonction de l’ellipsoide choisie. Et il y a un grand nombre d’ellipsoides potentiellement utilisables parce que certaines ellipsoides approximent mieux le géoide à certains endroits de la Terre qu’à d’autres (Figure 3). Sur la figure 3 par exemple, on se rend compte que l’ellipsoide n°1 est plus pertinente sur la partie gauche de la figure (elle coincide mieux avec le géoide) alors que l’ellipsoide n°2 est plus pertinente sur la partie droite de la figure.
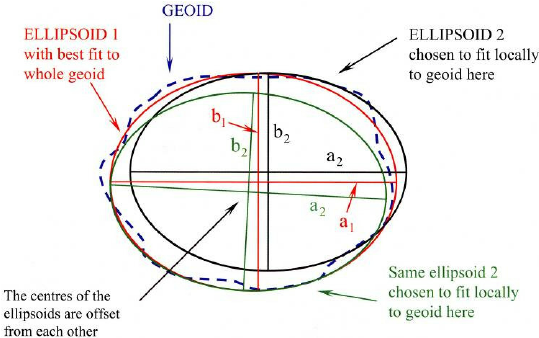
Figure 3. Géoide et ellipsoides. Les longueurs a et b permettent de caractériser une ellipsoide
Une fois que l’on a choisi notre géoide et notre ellipsoide de référence, on a donc enfin notre représentation de la Terre, et on peut commencer à parler de coordonnées ! On parle alors de système géodésique (ou géographique) : un système avec un géoide, une ellipsoide, et des coordonnées associées.
Coordonnées cartésiennes
Dans un système géodésique dont les coordonnées sont présentées sous format cartésien, les coordonnées de chaque observation à la surface de la terre sont données dans un repère X,Y,Z ayant pour origine le centre de la Terre. Le plan XY est dans le plan de l’équateur, et l’axe X recoupe le méridien d’origine (dans la majorité des pays, ce méridien est celui de Greenwich). L’axe Z est l’axe qui va du centre de la Terre aux pôles. Dans le format cartésien, on ne parle donc pas de coordonnées en longitude ou latitude, on parle juste de coordonnées dans le plan XYZ que vous voyez sur la figure.
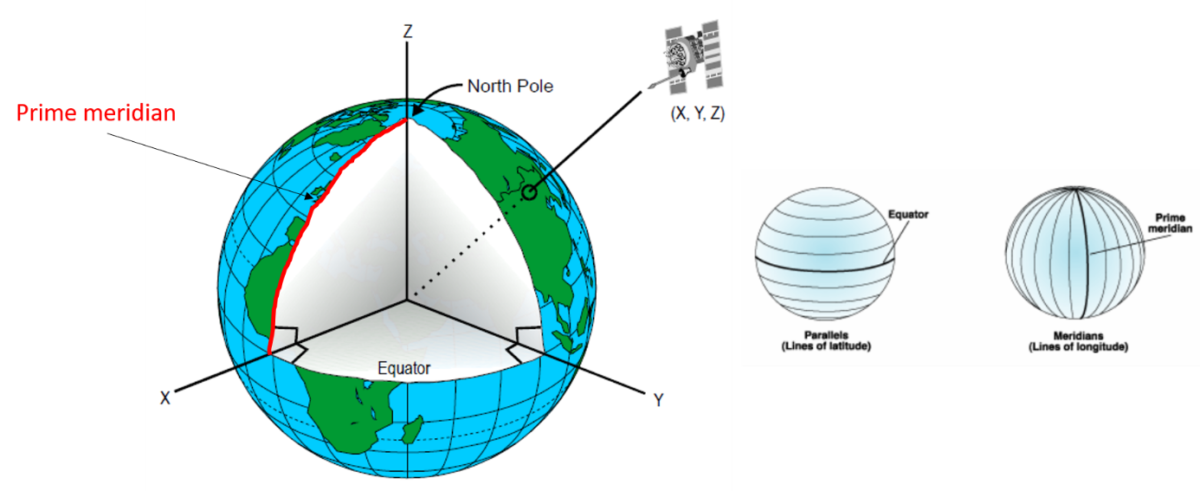
Figure 4. Système de coordonnées cartésiennes
Coordonnées géodétiques et géocentriques
Dans un système géodésique, on peut aussi présenter les coordonnées sous forme géodétique ou géocentrique, on commence alors à parler de longitude et de latitude ! Dans un système géodésique avec des coordonnées géocentriques, la latitude d’un point à la surface de la Terre est l’angle entre (i) le plan de l’équateur et (ii) l’axe qui part du centre de la Terre jusqu’au point d’observation (Figure 5). Les coordonnées sont dites géocentriques parce que la latitude est mesurée par rapport au centre de la Terre. Dans un système à coordonnées géodétiques, la latitude d’un point à la surface de la Terre est l’angle entre (i) le plan de l’équateur et (ii) l’axe perpendiculaire à l’ellipsoide de référence qui passe par le point d’observation (Figure 5). La seule différence par rapport aux systèmes de coordonnées sous format géodétique et géocentriques est leur définition de la latitude. Pour ces deux systèmes, la longitude d’un point est définie comme l’angle donné entre le méridian d’origine et le méridian qui passe par ce point. La figure 6 sera peut-être plus explicite pour clarifier comment se représenter les éléments de latitude et longitude.
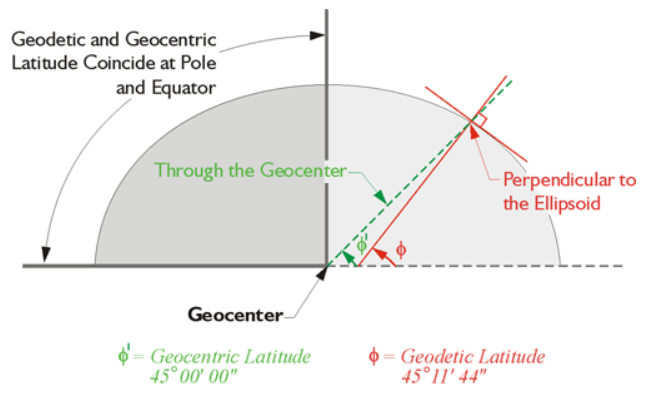
Figure 5. Définition de la latitude pour un système de coordonnées géocentrique et géodétique
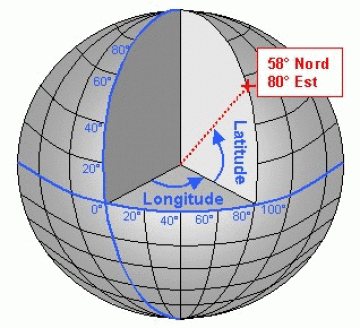
Figure 6. Longitude vs. Latitude
Notez que des équations existent pour passer d’un système de coordonnées cartésiennes à un système de coordonnées géodétique et/ou géocentrique.
Coordonnées non-projetées et coordonnées projetées
Là où il faut être très clair, c’est sur le fait que les coordonnées dans un système géocentrique ou géodétique sont exprimées sous des formes d’angles ! On ne peut donc pas calculer de distance entre deux points à la surface de la terre dans des systèmes de coordonnées géodétiques/géocentriques. Pour ce faire, il est nécessaire de projeter ces coordonnées (en degrés) sur une carte plane pour avoir des coordonnées métriques ! Je vous invite à aller regarder la courte vidéo de la chaine Vox qui explique ça de façon extrêmement claire et limpide.
Tout comme il existe un grand choix d’ellipsoides de référence, il existe un grand choix de supports sur lesquels on peut projeter des coordonnées géodétiques/géocentriques (Figure 7). Imaginez vous positionner votre représentation de la Terre dans un support cylindrique (Figure 7a). Projetez l’ensemble de vos coordonnées sur ce support cylindrique, découpez votre support cylindrique, et vous obtenez alors une surface plane sur laquelle vous avez vos coordonnées planaires (métriques). En fonction du support utilisé, vous aurez des cartes planes qui seront plus ou moins pertinentes en fonction de l’endroit où vous vous trouvez sur la Terre. Et ce n’est qu’une fois que vous aurez projeté vos coordonnées que vous pourrez calculer des notions de distance entre points sur votre carte. Attention donc quand vous parlez de longitude ou latitude si vous êtes dans un système de coordonnées géodétiques/géocentriques ou planaires !
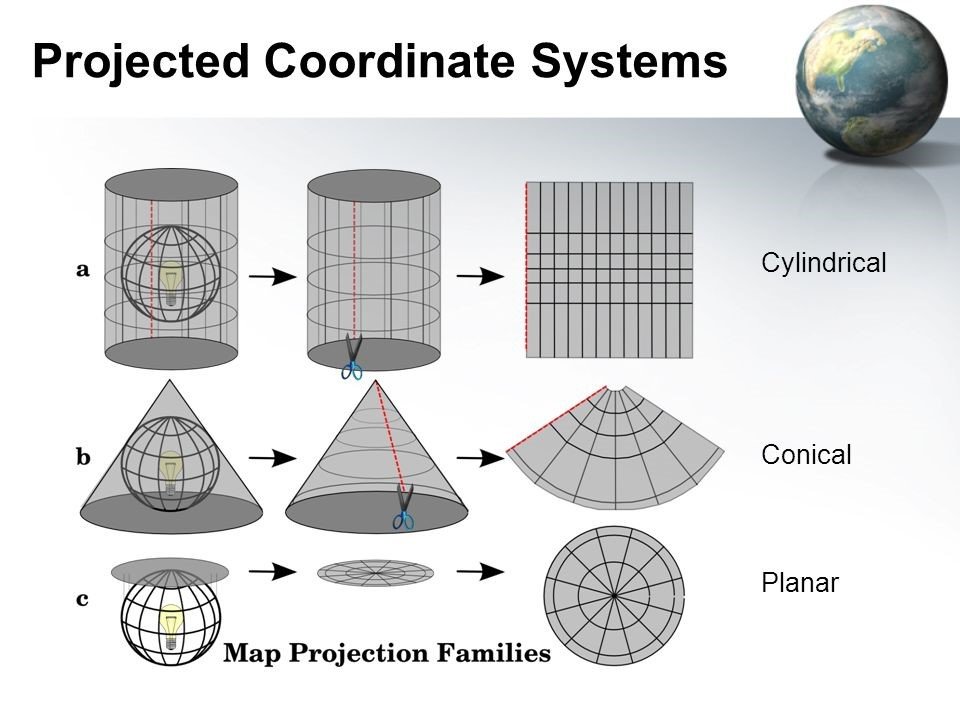
Figure 7. Systèmes de coordonnées projetées
WGS84 et Lambert 93
Prenons deux exemples pour essayer de recontextualiser tout ça :
- WGS84 : Vous avez très certainement déjà vu ou entendu parler de ce système de coordonnées de référence. Mais vous étiez-vous déjà demandé à quoi ça correspondait ? Et bien, WGS84 est un système géodésique mondial ! Les données ne sont donc pas projetées ! C’est un système géodésique à coordonnées géocentriques ou géodésiques basé sur le géoide EGM96, l’ellipsoide de référence IAG GRS80, et le méridien d’origine est celui de Greenwich. Notez que la plupart des systèmes de coordonnées projetées UTM (pour Universal Transverse Mercator) sont basés sur le système de coordonnées géocentriques/géodétiques WGS84
- Lambert 93 : En France, on entend souvent dire que les données sont en Lambert 93 mais, encore une fois, vous étiez-vous déjà demandé à quoi ça correspondait ? Lambert 93 est une projection conique (voir Figure 7) ! Elle est liée au système géodésique RGF93 – système basé sur l’ellipsoide de référence IAG GRS80, et le méridien de référence est le 3ème méridien à l’est par rapport à celui d’origine de Greenwich. On devrait donc plutôt parler du système de coordonnées RGF93-Lambert 93 si on voulait être précis. Jusqu’en 2001, en France, on utilisait le système géodésique NTF (Nouvelle Triangulation Francaise). Ce système géodésique était basé sur une ellipsoide différence, celle de Clarke 1880 IGN. Notez également que d’autres projections coniques conformes sont aussi utilisées pour limiter certains phénomènes d’altération linéaire de la projection Lambert 93 (notamment proche des frontières de la France – qui sont donc loin du barycentre de la France).
Pour ne pas faire de confusion entre les différents systèmes de coordonnées utilisées, un code unique a été associé à chaque système par l’European Petroleum Survey Group (EPSG). Le code EPSG du système géodésique WGS84 est 4326. Le code EPSG du système de coordonnées RGF93-Lambert 93 est 2154.
Lorsque vous êtes bien au clair sur le système de coordonnées associé à vos données, vous pouvez assez facilement reprojeter vos données dans un autre système de coordonnées au besoin à l’aide d’équations mathématiques spécifiques (déjà renseignées dans des outils cartographiques type QGIS ou dans des fonctions R/Python). Et vous pouvez ensuite vous intéresser à la précision de la localisation de vos données dans le système de coordonnées dans lequel vous les avez acquises. Vous aurez par exemple une précision différente en fonction des supports GNSS, DGPS ou RTK utilisés, mais ce n’est pas l’objet de ce post (peut-être d’un prochain !)
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?


2 commentaires sur « Les systèmes de coordonnées de référence »