Lorsque l’on s’intéresse aux géostatistiques, on a du mal à passer à côté du variogramme. L’utilisation de cet outil est soumise à plusieurs hypothèses fondamentales qui sont souvent présentées de manière très théorique. Ces hypothèses sont généralement mises de côté parce qu’elles sont relativement difficiles à comprendre. Je dois admettre que les équations mathématiques et la théorie en rapport avec ces hypothèses ne sont pas simplement expliquées ce qui fait que les non-spécialistes ne sont généralement même pas au courant de leur existence. Ce post a pour objectif de fournir une description plus abordable (je l’espère) de ces hypothèses et du vocabulaire spécifique associé.
Qu’est ce qu’une variable régionalisée ?
La géostatistique s’intéresse à l’étude de ce que l’on appelle les variables régionalisées. Ces variables régionalisées, que l’on appelle souvent Z, sont des fonctions définies sur un domaine d’étude (une parcelle par exemple) et dont l’objectif est de représenter l’évolution d’un phénomène sur ce domaine d’étude (ex: le rendement, la teneur du sol en nutriments…). Il est considéré que tous les échantillons disponibles sur ce domaine d’étude ont été générés par le processus Z. A chaque position connue x_i dans la parcelle (la position des échantillons), Z(x_i) est défini et chaque Z(x_i) est considéré comme une variable aléatoire qui est dite être une réalisation de Z à la position x_i. Comme une seule valeur est connue pour chacune de ces variables aléatoires (il y a seulement un échantillon à la position x_i), il n’est pas possible de caractériser la fonction Z. En effet, chaque variable aléatoire Z(x_i) a sa propre loi de distribution. Est ce que cela signifie que les variables régionalisées ne peuvent pas être étudiées ? N’ayez pas peur ! Des hypothèses ont été mises en place et elles seront explicitées plus en détail dans la suite de ce post. Deux indices néanmoins : la stationnarité d’ordre 2 et la stationnarité intrinsèque.
Les variables régionalisées présentent généralement un composant structuré spatialement et un autre aléatoire. La structure spatiale correspond aux patrons spatiaux dans la parcelle (ex: le fait que les valeurs de rendement semblent plus fortes dans la partie sud que dans la partie nord de la parcelle) alors que l’effet aléatoire peut être relié au bruit ou aux variations à courtes distances au sein de la parcelle. Cet effet aléatoire est défini comme l’effet pépite dans le variogramme.
Stationnarité d’ordre 2: un des hypothèses de base du variogramme
Dans chaque livre et dans chaque post en rapport avec le variogramme, la stationnarité d’ordre 2 y est présentée comme une des hypothèses fondatrices. Mais qu’est ce que cela veut bien dire? Qu’est ce que cette hypothèse implique? Tout d’abord, il faut comprendre que le terme de stationnarité d’ordre 2 s’applique à la fonction Z(x) et pas aux données. Z(x) est dit stationnaire d’ordre 2, pas les données ! Un variogramme remplit les conditions de stationnarité d’ordre 2 si Z(x) est stationnaire d’ordre 2 et respecte donc les règles suivantes:
- L’espérance et la variance de Z(x), respectivement E[Z(x)] et Var[Z(x)], sont constantes sur tout le domaine d’étude, c’est à dire qu’elles ne dépendent pas de la position x des observations dans la parcelle
- La covariance entre les observations séparées par une distance h, cov(Z(x+h),Z(x)), dépend seulement de la distance h entre ces observations et pas de la position x des observations dans la parcelle
La première hypothèse assume que pour un nombre fini d’échantillons x_1, x_2,...., x_n et pour n’importe quelle distance h, la distribution de Z(x_1), Z(x_2),...., Z(x_n) devrait être la même que celle de Z(x_1+h), Z(x_2+h),...., Z(x_n+h). De ce fait, on peut assumer que E[Z(x)]=\mu (une constante) et Var[Z(x)]=\sigma^{2} (aussi une constante). Cette hypothèse est importante pour certaines formes de krigeage.
La deuxième hypothèse permet de définir la fonction de covariance C(h) qui équivaut à cov(Z(x+h),Z(x)) parce que la position spatiale des observations (x) n’a pas d’influence sur la relation entre les observations. Si la covariance entre deux observations évoluait dans la parcelle en fonction de la position de ces observations, il ne serait pas possible de définir clairement Z(x) puisque chaque Z(x_i) correspond seulement à une réalisation de Z(x). Il faut bien comprendre que l’existence de la fonction de covariance C(h) dépend de cette deuxième hypothèse.
Stationnarité intrinsèque
Pour définir le variogramme, une dernière hypothèse doit être faite, celle de stationnarité intrinsèque. Ce postulat considère que la variable Z(x+h)-Z(x) est stationnaire. Il faut bien noter ici qu’on ne s’intéresse pas seulement à la variable Z(x) mais bien à la différence Z(x+h)-Z(x). A partir de cette hypothèse de stationnarité, on peut assumer que la variance de Z(x+h)-Z(x) n’est plus dépendante de la position x des observations mais seulement de la distance entre elles. Par conséquent, il est possible d’écrire l’équation suivante:
Var(Z(x+h)-Z(x)=2f(h)
La variance de cette différence entre variable peut être synthétisée par la fonction f qui est donc seulement dépendante de la distance h entre deux observations. Rappelez-vous que le variogramme est l’outil qui permet d’étudier l’évolution de la variance entre deux observations séparées par une distance h. En réalité, la fonction f n’est rien d’autre que la fonction de variance γ(h) qui définit le variogramme. On peut donc écrire :
Var(Z(x+h)-Z(x)=2\gamma(h)
Relations entre le variogramme et la covariance
Ici, la relation entre la variance γ(h) et la fonction de covariance C(h) sera démontrée pour mettre en avant l’importance des hypothèses qui ont été présentées précédemment. Cette section contient pas mal d’équations mathématiques mais la démonstration est très détaillée ce qui devrait permettre de se lancer dedans sans trop de problème. La fonction de variogramme a été définie dans le paragraphe précédent comme suit:
2\gamma(h)=Var(Z(x+h)-Z(x)
Pour une variable X, les propriétés de variance nous disent que :
Var(X)=E([X-E(X)]^{2})
Où E est l’espérance de la variable X
Par conséquent, pour la variable Z(x+h)-Z(x), la fonction de variogramme peut être réécrite comme suit :
2\gamma(h)=E([Z(x+h)-Z(x)-E(Z(x+h)-Z(x))]^{2})
Comme Z(x) est une variable stationnaire, E[Z(x)]=E[Z(x+h)]. On peut en conclure que E[Z(x+h)-Z(x)]=0 d’après les propriétés de l’espérance. En effet, on peut rappeler que pour deux variables X et Y, E(X+Y)= E(X)+E(Y). La fonction de variogramme peut donc être simplifiée:
2\gamma(h)=E([Z(x+h)-Z(x)]^{2})
En ajoutant et soustrayant \mu , l’espérance de Z(x), on peut écrire:
2\gamma(h)=E([(Z(x+h)-\mu)-(Z(x)-\mu)]^{2})
En développant le terme au carré, il vient:
2\gamma(h)=E([Z(x+h)-\mu]^{2}+[Z(x)-\mu]^{2}-2[Z(x+h)-\mu][Z(X)-\mu])
D’après les propriétés de l’espérance, à savoir que E(X+Y)=E(X)+E(Y), on peut écrire:
2\gamma(h)=E([Z(x+h)-\mu]^{2})+E([Z(x)-\mu]^{2})-2E([Z(x+h)-\mu][Z(X)-\mu])
Ici, on reconnait la covariance entre les variables Z(x+h) et Z(x) dans le dernier terme,
2\gamma(h)=E([Z(x+h)-\mu]^{2})+E([Z(x)-\mu]^{2})-2cov[Z(x+h),Z(h)]
Comme Z(x) est stationnaire d’ordre 2, la covariance entre Z(x+h) et Z(x) est définie par C(h),
2\gamma(h)=E([Z(x+h)-\mu]^{2})+E([Z(x)-\mu]^{2})-2C(h)
Précédemment, \mu a été définie comme l’espérance de Z(x). Comme Z(x) est une variable stationnaire d’ordre 2, on a E[Z(x)]=E[Z(x+h)] et il vient :
2\gamma(h)=E([Z(x+h)-E(Z(x+h))]^{2})+E([Z(x)-E(Z(x))]^{2})-2C(h)
On reconnait également la formule de variance:
2\gamma(h)=Var(Z(x+h))+Var(Z(x))-2C(h)
Z(x) est stationnaire d’ordre 2 donc la variance de Z(x) est constante sur tout le domaine d’étude :
2\gamma(h)=\sigma^{2}+\sigma^{2}-2C(h)
2\gamma(h)=2\sigma^{2}-2C(h)
\gamma(h)=\sigma^{2}-C(h)
Tout l’objectif de la démonstration était d’établir la relation entre la variance \gamma(h) et la covariance C(h) entre observations séparées par une distance h (Fig. 1). Il faut bien comprendre que si la covariance existe, alors la variance \gamma(h) existe également. Attention, le contraire n’est pas vrai ! Pour que la covariance existe, il faut que Z(x) soit considérée stationnaire d’ordre 2. Il faut accepter l’hypothèse de stationnarité intrinsèque pour pouvoir définir le variogramme. Notez que le variogramme peut être défini même si l’hypothèse de stationnarité d’ordre 2 de Z(x) n’est pas acceptée. Cependant, dans ce cas, la covariance ne sera pas définie.
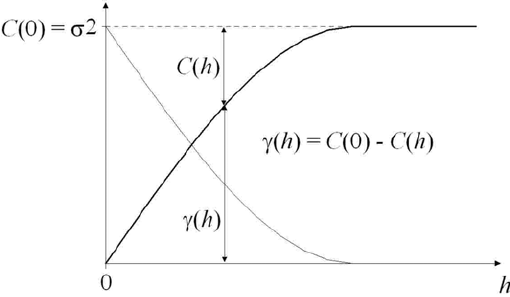
Fig. 1 Relation entre la semi-variance et la covariance
D’un point de vue plus pratique, Z(x) peut être considérée stationnaire d’ordre 2 si la variance \gamma(h) atteint un pallier. A noter également que le variogramme est défini pour tout le domaine d’étude ce qui signifie que la fonction de variogramme est considérée comme vraie sur toute la parcelle. Dans le cas de structures spatiales emboitées, il est possible d’assumer la stationnarité sur une partie du domaine d’étude (stationnarité jusqu’à une distance h fixée).
Stationnarité et stationnarité d’ordre 2
Ces deux concepts ne se rapportent pas aux mêmes hypothèses et il ne faut pas faire de confusion entre les deux termes. Une variable stationnaire Z(x) est une variable donc la moyenne et la variance sont invariants par translation, ce qui veut dire que la moyenne et variance sont constants sur le domaine d’étude. Ces métriques ne dépendent pas de la position x des observations sur le domaine. L’hypothèse de stationnarité de second ordre ajoute que la covariance entre deux observations séparées par une distance h, c’est à dire cov(Z(x+h),Z(x)) dépend seulement de la distance h entre ces observations. Il faut comprendre que l’hypothèse de stationnarité n’implique pas celle de stationnarité de second ordre. L’hypothèse de stationnarité d’ordre 2 et de stationnarité intrinsèque sont utilisées pour que la fonction de covariance puisse être définie.
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

