When entering the field of geostatistics, one is confronted almost instantaneously to the variogram tool. The definition and existence of the variogram relies on fundamental assumptions that are often presented from a theoretical point of view. These assumptions are almost always left apart because they are relatively difficult to understand. I sincerely admit that the mathematical equations and the theory regarding these assumptions are not simply explained which makes non-specialists mostly unaware of them. This post intends to provide a more comprehensive description of the assumptions and related terminologies.
What is a regionalized variable ?
Geostatistics aims at studying what is called regionalized variables. These regionalized variables, often referred to as Z, are functions that are defined over a study domain (ex : a field) and whose objective is to represent the evolution of a phenomenom (ex: the yield, the soil nutrient content). All the samples available inside the field can be considered to have been generated by the process Z. At each known position Z(x_i) inside the field (the position of the samples), the Z(x_i) are random variables that are said to be, for each of them, a realization of Z at position x_i . As only one value is known for each random variable (there is only one sample at position x_i), it is not possible to characterize the function Z as such. Indeed each random variable Z(x_i) has it own probability distribution. Does this mean that regionalized variables cannot be studied ? Don’t be afraid ! Some assumptions have been put into place and will be discussed in the next section. Two clues : second-order stationarity and intrinsic stationarity.
Regionalized variables exhibit a spatially-structured component and a random one. The spatial structure corresponds to the spatial patterns within the field (ex: yield values seem stronger in the southern part of the field than in the northern part) while the random effect can be related to the noise or the small-scale variations inside the field. This random component is defined by the nugget effect of the variogram.
Second-order stationarity: the foundation of the variogram
In every book and post related to the variogram, the second-order stationarity is said to be a fundamental assumption. But what does this mean? What does it imply? First of all, it must be understood that the term second order stationarity applies to the function Z(x) and not to the data. Z(x) is said second-order stationary, not the data ! A variogram fullfills the requirements of second-order stationarity if Z(x) is second-order stationary and as such respects the following rules :
- The expectation and variance of Z(x), respectively E[Z(x)] eandVar[Z(x)], are constant over the entire study domain, that is to say that they do not depend on the location x inside the field
- The covariance between two observations separated by a distance h, cov(Z(x+h),Z(x)), only relies on the distance h between the observations and not on the spatial location x inside the field
First assumption states that for a finite number of samples x_1, x_2,...., x_n and for any distance lag h, the distribution of Z(x_1), Z(x_2),...., Z(x_n) would be the same as that of Z(x_1+h), Z(x_2+h),...., Z(x_n+h). As such, it can be assumed that E[Z(x)]=\mu (a constant) and Var[Z(x)]=\sigma^{2} (also a constant). This assumption is important to make for some kriging procedures.
Second assumption enables to define the covariance function C(h) which is equal to cov(Z(x+h),Z(x)) because the spatial position (x) of the observations has no influence on the relationships between two observations. If the covariance between two observations was evolving in the field in relation to the positions of the observations inside the field, it would not be possible to define clearly the function Z(x) as each Z(x_i) is only one realization of Z(x). It must be understood that the existence and the definition of the covariance function C(h) relies on this second assumption.
Intrinsic stationarity
To be able to define the variogram, one more assumption needs to be stated, that of intrinsic stationarity. This hypothesis considers that the variable Z(x+h)-Z(x) is stationary. Note that here, we are not interested only in Z(x) but in the difference Z(x+h)-Z(x). From this assumption of stationary, it can be assumed that the variance of Z(x+h)-Z(x) is no longer dependent on the position x of the observations but only rely on the lag distance between them. As a consequence, the following equation can be derived:
Var(Z(x+h)-Z(x)=2f(h)
The variance of this difference can be synthetized by the function f that is only dependent on the lag distance h between two observations. Remind that the variogram is defined as the evolution of the variance between observations separated by a distance h. Actually, the function f is nothing else that the variance between observations γ(h) that gives birth to the variogram. Hence:
Var(Z(x+h)-Z(x)=2\gamma(h)
Relationship between the semi-variance and the covariance
In this section, the relation between the semi-variance function γ(h) and the covariance function C(h) will be demonstrated to show the importance of all the assumptions that were set before. This section contains lots of mathematical equations but the demonstration is very detailed and should be understood relatively easily. The variogram function has been defined in the previous section as:
2\gamma(h)=Var(Z(x+h)-Z(x)
The variance properties state that, for a variable X :
Var(X)=E([X-E(X)]^{2})
Where E(X) is the expectation of the variable X.
As a consequence, regarding the variable Z(x+h)-Z(x), the variogram function can be rewritten as follows:
2\gamma(h)=E([Z(x+h)-Z(x)-E(Z(x+h)-Z(x))]^{2})
Because Z(x) is a second-order stationary variable, E[Z(x)]=E[Z(x+h)]. For two variables X and Y, it can be said that E(X+Y)= E(X)+E(Y) which means that E[Z(x+h)-Z(x)]=0 and that the variogram function can be simplified :
2\gamma(h)=E([Z(x+h)-Z(x)]^{2})
By adding and subtracting \mu , the expectation of Z(x), it can be written:
2\gamma(h)=E([(Z(x+h)-\mu)-(Z(x)-\mu)]^{2})
When developing the squared term,
2\gamma(h)=E([Z(x+h)-\mu]^{2}+[Z(x)-\mu]^{2}-2[Z(x+h)-\mu][Z(X)-\mu])
The expectation properties state that E(X+Y)=E(X)+E(Y). As such:
2\gamma(h)=E([Z(x+h)-\mu]^{2})+E([Z(x)-\mu]^{2})-2E([Z(x+h)-\mu][Z(X)-\mu])
Here, the last term refers to the covariance between the variables Z(x+h) and Z(x), so:
2\gamma(h)=E([Z(x+h)-\mu]^{2})+E([Z(x)-\mu]^{2})-2cov[Z(x+h),Z(h)]
Given that Z(x) is a second-order stationary variable, the covariance between Z(x+h) and Z(x) is defined as C(h),
2\gamma(h)=E([Z(x+h)-\mu]^{2})+E([Z(x)-\mu]^{2})-2C(h)
Previously, \mu was defined as the expectation of Z(x). As Z(x) is a second order stationary variable, E[Z(x)]=E[Z(x+h)] and :
2\gamma(h)=E([Z(x+h)-E(Z(x+h))]^{2})+E([Z(x)-E(Z(x))]^{2})-2C(h)
One can recognize the variance formula:
2\gamma(h)=Var(Z(x+h))+Var(Z(x))-2C(h)
Z(x) is second-order stationary so the variance Z(x) is constant over the entire study domain so:
2\gamma(h)=\sigma^{2}+\sigma^{2}-2C(h)
2\gamma(h)=2\sigma^{2}-2C(h)
\gamma(h)=\sigma^{2}-C(h)
All the purpose of the definition was to establish the relation between the variance \gamma(h) and the covariance C(h) between observations separated by a lag distance h (Fig. 1). It must be understood that if the covariance exists, then the semi-variance \gamma(h) between observations exists. However, the opposite reasoning is wrong. For the covariance to exist, Z(x) must be considered as a second-order stationary variable. The intrinsic stationary also has to be assumed so that the variogram can be derived! Be aware that the variogram can still be defined even if Z(x) is not a second-order stationary variable. However, in that case, the covariance will remain undefined. Even if all the demonstration is not clear for you, what must be understood is that these assumptions regarding the different types of stationarity of Z(x) are fundamental so that the semi-variance and covariance functions can exist.
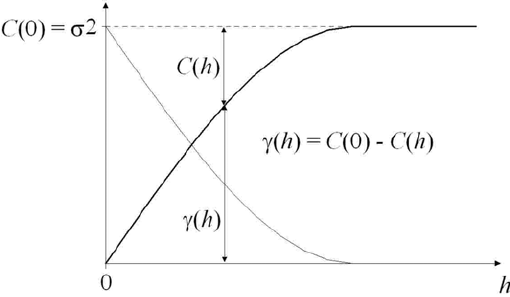
Fig. 1. Relationship between the semi-variance and the covariance
From a more practical point of view, Z(x) can be considered second-order stationary if the semi-variance \gamma(h) reaches a plateau. In case of nested spatial structures, the stationarity can be assumed at specific spatial scales for simplification purposes. Note also that the variogram is defined for the whole study domain which means that the variogram function is considered true over the whole field.
Stationarity and second order stationarity
These two concepts do not refer to the same assumptions and there must be no confusion between those two terms. A stationary variable Z(x) is a variable whose mean and variance are invariant by translation, which means that the mean and variance are constant over the whole domain. Second-order stationarity assumes in addition that the covariance between observations separated by a lag h, that is to say cov(Z(x+h),Z(x)) only depends on the lag h between these observations. It must be understood that stationarity does not imply second-order stationarity. The assumptions of second-order stationarity and intrinsic stationarity are made so that a covariance function can be defined.
Support Aspexit’s blog posts on TIPEEE
A small donation to continue to offer quality content and to always share and popularize knowledge =) ?

