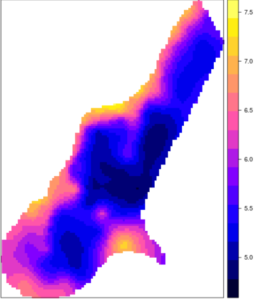
Figure 0. Carte interpolée de teneur en zinc du sol

L’interpolation est le procédé qui vise à cartographier une variable V_0 à des positions dans l’espace où aucun échantillon n’est disponible en utilisant un jeu de données d’échantillons dont la position dans l’espace et la valeur de la variable V_0 sont connues (Fig. 1). Ces échantillons peuvent provenir d’une campagne d’échantillonnage sur le terrain ou peuvent être des informations issues de capteurs fixes ou mobiles à l’intérieur d’une parcelle. Généralement, dans les études d’agriculture de précision, un ensemble d’informations est disponible au sein d’une parcelle (les échantillons) et l’objectif est de construire une carte de cette information sur la totalité de la parcelle. En général, seuls quelques échantillons sont disponibles parce que les campagnes de terrain sont pénibles et chronophages ou parce que le déploiement d’une grande quantité de capteurs serait beaucoup trop cher à mettre en oeuvre. Bien sûr, il n’est de toute façon pas possible de collecter des informations sur chaque centimètre carré de parcelle par échantillonnage. C’est pour cela que les méthodes d’interpolation ont tout leur intérêt. Plusieurs techniques d’interpolation existent mais il est quelquefois difficile de comprendre les avantages et inconvénients de chacune des approches. Ce post a pour objectif de présenter les méthodes d’interpolation spatiale les plus utilisées, en tentant de clarifier les avantages, défauts et différences entre ces approches.

Figure 1. Principe de l’interpolation

Les techniques d’interpolation spatiale peuvent être séparées en deux principales catégories : les approches déterministes et géostatistiques. Pour faire simple, les méthodes déterministes n’essayent pas de capturer la structure spatiale des données. Elles utilisent seulement des équations mathématiques prédéfinies pour prédire des valeurs à des positions où aucun échantillon n’est disponible (en pondérant les valeurs attributaires des échantillons dont la position dans la parcelle est connue). Au contraire, les méthodes géostatistiques cherchent à ajuster un modèle spatial aux données. Cela permet de générer une valeur prédite à des positions non échantillonnées dans la parcelle (comme les méthodes déterministes) et de fournir aux utilisateurs une estimation de la précision de cette prédiction. Les méthodes déterministes regroupent les approches TIN, IDW et d’analyses de tendance de surface. Les approches géostatistiques regroupent le krigeage et ses dérivés. Toutes les méthodes qui seront discutées doivent être appliquées sur des variables continues (NDVI, rendement, teneur en carbone du sol) et pas factoriel (ex : une classe issue d’une méthode de classification) ou binaires (variables avec des valeurs de 0 ou 1 – il existe des méthodes pour ce type de données, notamment des méthodes de krigeage – Indicator Kriging – mais nous n’en parlerons pas ici).

Toutes les méthodes d’interpolation sont basées sur le fait que les données spatiales sont auto-corrélées. En fait, “everything is related to everything else, but near things are more related than distant things” (Tobler, 1970)  ¹. Tout est relié à tout le reste, mais les choses proches partagent plus de caractéristiques que des choses distantes. Les méthodes d’interpolation peuvent être utilisées pour prédire des valeurs à des positions spécifiques dans l’espace ou peuvent être utilisées sur une grille d’interpolation sur l’ensemble de la parcelle considérée. Cette grille est composée de pixels régulièrement espacés dont la taille peut dépendre de la précision recherchée dans la carte interpolée ou bien de la structure spatiale du jeu de données

TIN : Interpolation par triangulation irrégulière

L’approche par TIN est peut être l’une des techniques d’interpolation spatiale les plus simples. Cette approche s’appuie sur la construction d’un réseau triangulaire (un cas particulier de tesselation) basé sur la position spatiale des échantillons disponibles. Plusieurs méthodes de triangulation peuvent être utilisées mais celle de Delaunay est la plus utilisée (Fig. 2). Cette méthode a pour objectif de créer des triangles qui ne se chevauchent pas (et aussi équilatéral que possible) et dont le cercle circonscrit contient seulement les trois sommets qui ont donné naissance au triangle. Une fois que le réseau est opérationnel, chaque nouvelle observation z_i pour laquelle une nouvelle valeur attributaire doit être prédite, est associée à un triangle T dans lequel cette observation se trouve. Cette valeur attributaire est calculée en pondérant les valeurs attributaires des sommets du triangle T.

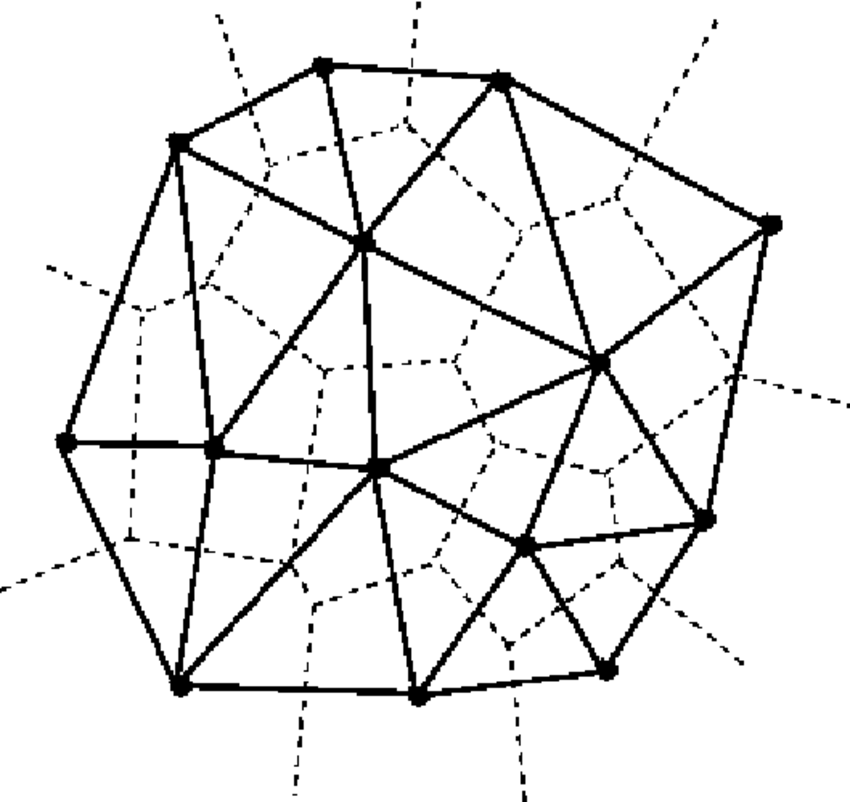
Figure 2. Création d’un réseau triangulaire: la triangulation de Delaunay

Il est clair que la précision de cette méthode dépend du nombre d’observations dans la parcelle, et plus particulièrement de la densité de ces observations. Quand les échantillons sont regroupés spatialement, les valeurs attributaires des observations voisines seront relativement bien prédites. Par contre, pour des échantillons isolés, les triangles construits seront beaucoup plus grands ce qui rendra la prédiction sur des observations voisines assez imprécise. Il faut se rappeler que la valeur à prédire de chaque nouvelle observation z_i dépend uniquement de la valeur attributaire des sommets du triangle dans lequel se trouve z_i.

Effectivement, cette technique d’interpolation ne participe pas vraiment au lissage des données. La technique TIN est disponible sur de nombreux logiciels et est efficace d’un point de vue du temps de calcul. Elle peut être utilisée lorsqu’un très grand nombre d’observations est disponible tout en ne demandant pas un gros espace mémoire. A noter que le réseau qui a été créé est aussi intéressant parce qu’il donne une information sur l’aire d’influence de chaque observation. Dans ce cas, d’autres tesselations comme les polygones de Thiessen sont particulièrement intéressants.

IDW : Pondération inverse à la distance

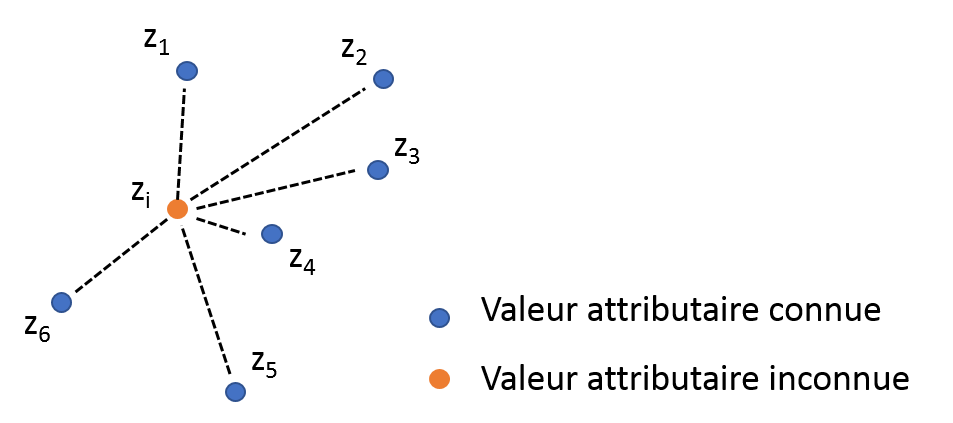
Figure 3. Pondération inverse à la distance. z_4 aura plus d’influence que z_2 sur z_i au vu des distances de z_2 et z_4 à z_i

Comme le nom le laisse à penser, la technique IDW permet de prédire la valeur attributaire d’une variable à des positions ou aucun échantillon n’est disponible en fonction de la distance spatiale entre cette position et d’autres positions où des échantillons ont été collectés (Fig. 3). Les observations les plus proches spatialement de l’observation à prédire reçoivent un poids plus important dans la prédiction alors que les observations éloignées auront une influence relativement faible sur la prédiction. Le poids attribué à chaque échantillon est aussi contrôlé par un paramètre de puissance, souvent dénommé p. Lorsque p augmente, le poids attribué aux échantillons éloignés décroit. Ce facteur peut être compris comme un paramètre de lissage. Si l’effet de lissage est trop important, cela peut cacher des variabilités intéressantes ou donner l’impression que la variable à prédire est beaucoup plus homogène sur la parcelle que ce qu’elle n’est vraiment. En fait, lorsque p est faible, les échantillons voisins et éloignés exercent une influence forte sur les observations à prédire. Par conséquent, la prédiction risque d’être très lissée parce qu’elle ne prend pas en compte que des phénomènes locaux. D’un autre côté, si p est trop grand, seuls les processus très locaux seront pris en compte ce qui pourra donner à la carte interpolé un aspect granulaire, non lisse. Un avantage par rapport à la méthode TIN et que la technique IDW prend en compte plus d’observations pour réaliser les préditions ce qui est susceptible d’améliorer la précision de ces dernières. Néanmoins, il est nécessaire de régler correctement le paramètre p pour que la carte interpolée soit pertinente et fiable. Comme la méthode TIN, l’approche par IDW est relativement facile à mettre en place et est largement disponible sur les logiciels d’usage (QGIS, ArcGIS, SAGA GIS…) et sur les languages de programmation (R, Python, Matlab…)

Analyse de tendance de surface

L’analyse de tendance de surface a pour objectif d’ajuster une tendance aux données. En d’autres termes, l’idée est de trouver l’équation qui passe au plus près des valeurs attributaires des échantillons disponibles. L’analyse de tendance de surface met souvent en jeu des régressions linéaires multiples ou des fonctions polynomiales pour trouver une relation entre la variable à prédire et une combinaison particulière des coordonnées spatiales. Certaines fonctions polynomiales peuvent être relativement complexes, d’ordre 4 ou 5 (y=aX^{4}+bX^{3}+cX^{2}). Cette approche est globale dans le sens où elle prend en compte tous les échantillons disponibles pour ajuster les régressions linéaires ou les fonctions polynomiales. Des approches plus locales peuvent être néanmoins mises en place pour améliorer les prédictions. A noter que l’analyse de tendance de surface peut souffrir de la présence d’outliers (données aberrantes). En fait, une observation aberrante est susceptible d’affecter sérieusement le modèle proposé ce qui peut conduire à un mauvaise ajustement du modèle aux données. Pour rendre l’analyse de tendance de surface fiable, il est important d’étalonner le modèle d’ajustement et ensuite de le valider. Pour ce faire, un jeu de données échantillonnés d’apprentissage doit être utilisé pour créer le modèle et un jeu de données échantillonnés de validation (indépendant du jeu d’apprentissage) doit servir à la validation du modèle. L’utilisation de jeux de données d’apprentissage et de validation est fondamental pour évaluer la pertinence et la précision du modèle proposé.

Toutes les approches déterministes décrites précédemment sont largement reportées et utilisées parce qu’elles sont relativement simples à comprendre et à mettre en place. Néanmoins, toutes ces méthodes prennent seulement en compte la distance spatiale entre les observations pour réaliser les prédictions. Aucune d’entre elles n’a pour objectif de capturer la structure spatiale des données ou de considérer les patrons spatiaux susceptibles d’être présents dans les parcelles. Le fait qu’aucun modèle spatial ne soit mis en place ne permet pas de rendre compte de la précision des prédictions dans la parcelle. Comme il l’a été précisé pour l’analyse de tendance de surface, en faisant usage de procédures de validation de modèle, il est possible de connaitre la précision des prédictions mais seulement là où des échantillons sont disponibles. Il n’est pas possible de construire une carte de précision de prédiction sur la totalité de la parcelle. Contrairement à ces méthodes déterministes, les approches géostatistiques permettent de mettre en place une carte d’erreur pour connaitre les endroits où les prédictions sont de qualité et les autres où la qualité est plus limitée.

Krigeage

Le krigeage est l’approche géostatistique la plus utilisée pour réaliser des interpolations spatiales. Les techniques de krigeage sont basées sur la définition d’un modèle spatial entre les observations (défini par un variogramme) pour prédire les valeur attributaires d’une variable à des positions où aucun échantillon n’est disponible. Une des spécificités du krigeage est qu’il ne considère pas seulement la distance entre les observations (comme pour les méthodes déterministes) mais qu’il essaye aussi de capturer la structure spatiale des données en comparant deux à deux les observations séparées par des distances spatiales spécifiques. L’objectif est de comprendre les relations existantes entre les observations séparées par des distances différentes dans l’espace. Toute cette information est prise en compte par le variogramme. Les méthodes de krigeage utilisent cette information pour attribuer un poids à chaque échantillon avant de réaliser les prédictions. Il faut noter que les techniques de krigeage permettent de préserver les valeurs attributaire des échantillons sur la carte interpolée.

Les méthodes de krigeage considèrent que le processus qui a donné naissance aux données peut être séparés en deux composantes principales : une tendance déterministe (les variations à large échelle) et une erreur auto-corrélée (les résidus):

Z(s)=m+e(s)

Où Z(s) est la valeur attributaire à la position s dans la parcelle, m est la tendance déterministe qui ne dépend pas de la position des données dans l’espace et e(s) qui est le terme d’erreur auto-corrélée (qui dépend de la position s). A noter que la tendance est déterministe ! Le variogramme est seulement calculé sur les résidus qui sont supposés être auto-corrélés ! En gros, quand on cherche à ajuster un modèle de variogramme aux données, on essaye en réalité d’ajuster ce modèle aux résidus de ces données, après que la tendance ait été enlevée. Attention au fait que, en fonction de la forme du variogramme, la carte interpolée peut être relativement lissée. En fait, si l’effet pépite est forte, les méthodes de krigeage auront tendance à lisser fortement les données pour réduire le bruit dans les parcelles. C’est parfois surprenant parce que l’étendue (écart entre minimum et maximum) des valeurs après krigeage est parfois plus faible que celle des échantillons de départ. Si l’effet pépite est effectivement très fort par rapport au pallier partiel, la structure spatiale est relativement faible et il serait peut être préférable de ne pas interpoler. Les dérivés du krigeage dépendent essentiellement de la façon dont la tendance est caractérisée. Ce point sera discuté en détail plus tard.

Grâce à l’utilisation du variogramme, une carte d’erreur peut être dérivée sur l’ensemble de la parcelle parce que les relations entre deux observations séparées par une distance h sont connues. La carte d’erreur est un outil très utile parce qu’elle donne accès à la qualité de la prédiction sur la totalité de la parcelle. Prenez en compte que la qualité de la carte d’erreur dépend bien évidemment de la qualité d’ajustement du modèle de variogramme aux données. Si ce modèle de variogramme n’est pas bien ajusté aux données, il y a de grands risques que la carte d’erreurs ne soit pas fiable. Attention également au fait que l’interpolation par krigeage est aussi sensible aux données aberrantes. Dans ce cas, ces outliers peuvent masquer l’auto-corrélation des données et empêcher la structure spatiale d’être mise en avant. Une solution intuitive serait d’enlever ces données aberrantes avant de réaliser le krigeage. Malgré tout, il est possible que certaines observations semblent aberrantes parce qu’elles sont beaucoup plus faibles ou fortes que le reste des observations. Si ces observations sont regroupées dans l’espace, cela pourrait être dû à un phénomène réellement existant au sein de la parcelle. Dans ce cas là, pour prendre en compte ce phénomène, mais pour ne pas empêcher la structure spatiale d’être découverte, une solution serait de calculer le semi-variogramme sans ces observations extrêmes et ensuite de réaliser le krigeage avec l’ensemble des informations. De cette manière, la structure spatiale serait bien évaluée et les données extrêmes seraient toujours prises en compte dans le jeu de données.

Krigeage simple

Comme le nom le laisse à penser, le krigeage simple est la méthode dérivée du krigeage la plus facile à mettre en oeuvre. Ici, la tendance déterministe, m, est connue et considérée constante sur la totalité de la parcelle d’étude (Fig. 4).

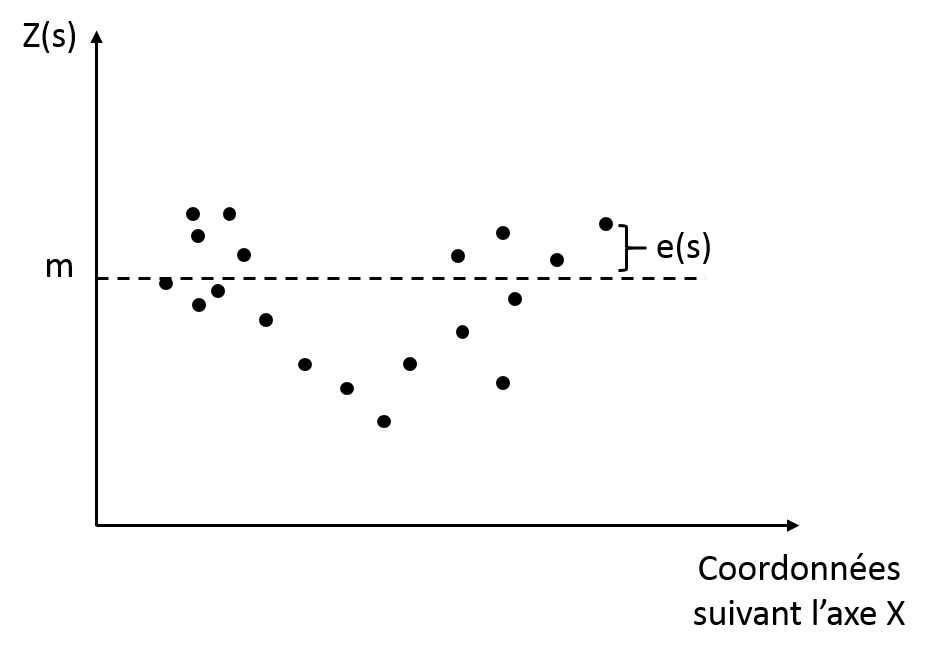
Figure 4. Krigeage simple et tendance et résidus correspondants

Cette méthode est globale parce qu’elle ne prend pas en compte les variations locales de cette tendance. Néanmoins, s’il n’y a pas de changements brusques dans les attributs de la variable d’intérêt (ou s’il n’y a pas de raisons qu’il n’y en ait), cette hypothèse peut être viable et pertinente. Comme la tendance est connue, le terme d’erreur auto-corrélée est lui aussi connu ce qui rend la prédiction plus simple à faire. Il doit être compris que, ici, les valeurs prédites ne peuvent pas s’étendre au-delà des valeurs des échantillons initiaux.

Krigeage ordinaire

Cette méthode est peut-être l’approche de krigeage la plus largement reportée. Contrairement au krigeage simple, cette technique considère que la tendance est constante mais seulement au niveau d’un voisinage local (Fig. 5). Cette hypothèse est intéressante parce qu’elle assure de prendre en compte les variations locales au sein d’une parcelle.

On pourrait imaginer par exemple qu’une rupture de pente au sein d’une parcelle serait intéressante à prendre en compte dans l’étude d’une variable d’intérêt.

Le krigeage ordinaire peut être exprimé de la façon suivante :

Z(s)=m(s)+e(s)

Ici, la tendance dépend de la position spatiale des observations (m(s)). Cette tendance constante est considérée inconnue et doit être déterminée à partir du voisinage de données correspondant.

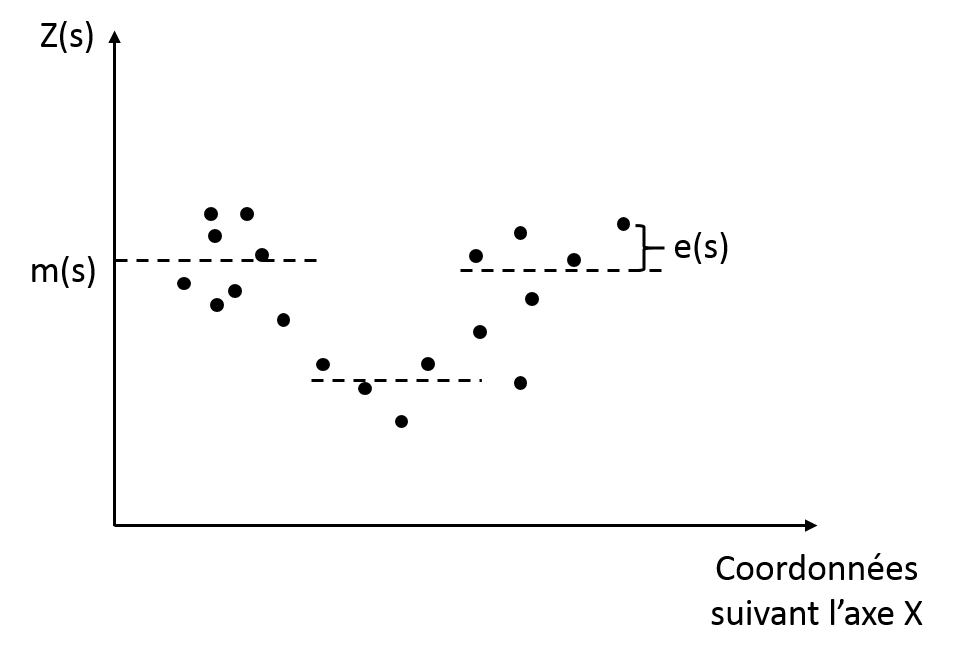
Figure 5. Krigeage ordinaire et tendance et résidus correspondants

Pour cette méthode, il est nécessaire de définir l’étendue du voisinage : le nombre d’observations voisines qui seront prises en compte pour chaque prédiction. Comme la tendance n’est pas considérée connue et qu’elle doive être déterminée par les données elles-mêmes, il peut arriver que, par construction, l’étendue des valeurs prédites soient plus larges sur celle des échantillons de départ.

Krigeage universel ou à tendance externe

Le krigeage par régression a plusieurs noms : le krigeage universel ou le krigeage avec une tendance externe. Cette méthode est similaire au krigeage ordinaire dans le sens où la tendance n’est pas constante sur la totalité de la parcelle mais dépend de la position des observations dans l’espace. Néanmoins, ici, la tendance est modélisée par une fonction plus complexe, elle n’est pas simplement considérée constante au sein d’un voisinage local (Fig. 6). L’objectif est le même que précédemment : enlever la tendance des données pour que les résidus auto-corrélés puissent être étudiés. A la fin de l’interpolation, la tendance est rajoutée aux résidus interpolés.

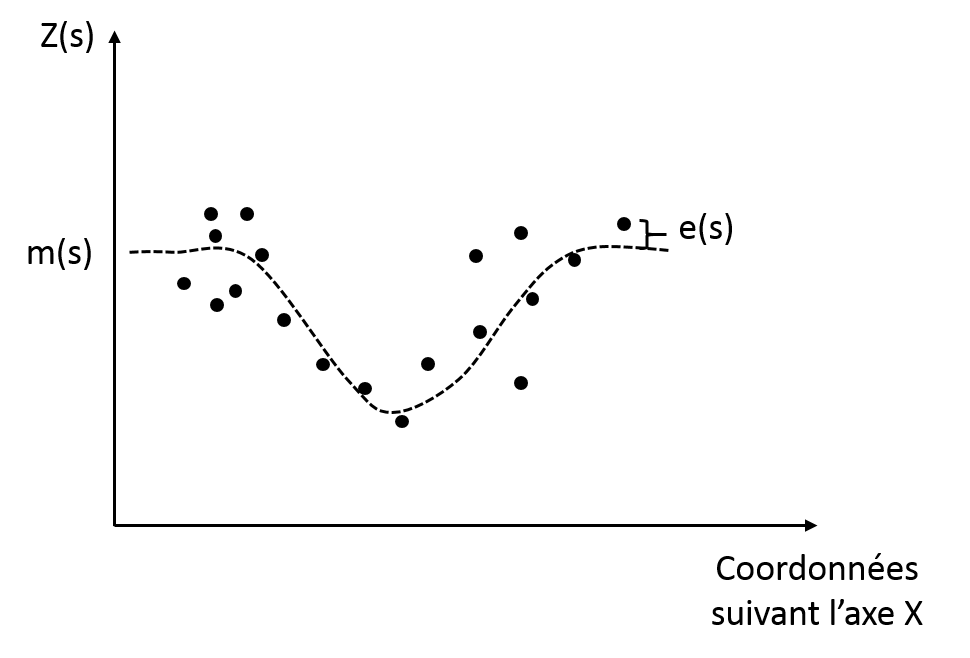
Figure 6. Krigeage par régression et tendance et résidus correspondants

Le krigeage par régression est intéressant lorsque l’on dispose d’une variable auxiliaire à haute résolution spatiale et qu’on voudrait avoir plus d’information sur une seconde variable pour laquelle seuls quelques échantillons sont disponibles. En général, cette deuxième variable est pénible, chère ou chronophage à obtenir. Dans ce cas, l’objectif est de modéliser la relation entre cette seconde variable et la variable auxiliaire de manière à améliorer les prédictions de la seconde variable.

Par exemple, l’information de biomasse est relativement facile à acquérir (à partir d’indices de végétation comme le NDVI obtenus avec des images satellites, avions ou drone). On pourrait imaginer utiliser cette variable auxiliaire pour aider à interpoler des observations de rendement collectées à une résolution spatiale beaucoup plus grossière pendant une campagne de terrain).

A noter que si la relation entre ces deux variables est faible, le krigeage par régression reviendra à réaliser un krigeage simple ou un krigeage ordinaire.

Co-krigeage

Lorsque l’on dispose d’une variable auxiliaire V0 avec une haute résolution spatiale et que l’on cherche à capturer la variabilité ou la corrélation spatiale d’une seconde variable V1, le co-krigeage est particulièrement intéressant. En fait, l’objectif est d’évaluer la structure spatiale de V1 par rapport à V0 avec les échantillons à disposition et d’interpoler la structure spatiale caractérisée sur l’ensemble de la parcelle. Comme il l’a été dit précédemment, V1 est généralement chronophage et coûteux à obtenir et il est beaucoup plus simple d’utiliser une variable auxiliaire pour améliorer les prédictions de V1. Le co-krigeage demande à l’utilisateur de calculer un cross-variogramme et d’y ajuster un modèle de variogramme. Dans ce cas, l’idée n’est pas d’étudier l’évolution de la variance d’une variable pour des distances spécifiques entre observations mais plutôt d’étudier l’évolution de la covariance de V1 par rapport à V0 pour ces distances spatiales particulières. En d’autres termes, on regarde comme la structure spatiale de V1 évolue par rapport à V0. On peut rajouter que le cross-variogramme est également un outil utile pour vérifier si deux variables sont corrélées spatialement ou si elles présentent une structure spatiale similaire. Dans ce cas-là, les deux variables peuvent avoir été acquises avec une haute résolution spatiale parce que l’objectif n’est plus de les interpoler mais de les comparer l’une par rapport à l’autre. Le co-krigeage est plus difficile à mettre en place que les autres techniques de krigeage mais il peut s’avérer plus efficace si les structures spatiales sont correctement déterminées.

Krigeage par point et krigeage par bloc

Toutes les méthodes de krigeage mentionnées précédemment ont pour vocation de prédire la valeur d’une variable d’intérêt à des positions où aucun échantillon n’est disponible. Ces positions peuvent être considérées comme des points dans l’espace (ou plus précisément comme des pixels de la grille d’interpolation avec un pixel = une valeur). Par conséquent, ces approches de krigeage peuvent être comprises comme des méthodes de krigeage par point. Quand l’incertitude de la prédiction est relativement large, on pourrait vouloir chercher à lisser les résultats interpolées en réalisant un krigeage sur une surface plus large qu’un tout petit pixel. Ce type de krigeage est connu sous le nom de krigeage par bloc. Cela a l’avantage de diminuer la variance de l’erreur de prédiction parce que l’information est plus grossière (elle est prédite sur un support spatial plus grand). Bien évidemment, avec le block kriging, il y a un risque de perdre de l’information utile mais quand l’incertitude est forte, cette approche peut être très pertinente.

Avant de terminer ce post, il est important de préciser que toutes les techniques d’interpolation qui ont été présentées produisent des résultats relativement similaires dans les cas idéaux (beaucoup d’échantillons disponibles et bien disposés dans la parcelle, peu de bruit dans les données et pas de variations brusques au sein de la parcelle). Néanmoins, quand ces conditions ne sont pas respectées, les méthodes géostatistiques sont intéressantes parce qu’elles permettent de capturer la structure spatiale sur l’ensemble de la parcelle, ce qui conduit généralement à des prédictions plus précises. Ces méthodes sont plus difficiles à mettre en place parce qu’il est nécessaire de construire un modèle spatial et de l’ajuster aux données mais cela peut permettre de mieux caractériser les parcelles. Encore une fois, je recommanderais de toujours garder une étape manuelle dans la mise en place d’approches géostatistiques parce que les résultats pourraient paraître étrange si les modèles spatiaux ne sont pas correctement ajustés aux données. Quand la structure spatiale est faible (lorsque le bruit est important), presque toutes les méthodes d’interpolation auront tendance à lisser les données dans une plus ou moins grande mesure. Cela doit être gardé à l’esprit avant d’interpoler des observations spatiales parce que les cartes interpolées pourraient paraître plus homogènes qu’elles ne le sont vraiment. On peut rajouter que les techniques d’interpolation peuvent être également utilisées pour sous-échantillonner (le plus souvent) ou sur-échantillonner une image ou une carte. L’objectif est de changer la résolution d’une carte ou d’une image disponible.

Par exemple, si une image de NDVI est acquise avec une résolution spatiale de 50cm, on pourrait vouloir sous-échantillonner cette image à une résolution spatiale de 5m pour avoir une représentation plus lissée de la carte finale.

Soutenez les articles de blog d’Aspexit sur TIPEEE

---

Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?