Présentation du variogramme
Il est presque impossible de parler d’analyse de données spatiales en Agriculture de Précision sans évoquer le variogramme. Prenez en compte que certaines personnes se réfèrent au terme semi-variogramme pour parler de la même chose. Il existe une confusion entre ces deux termes (Bachmaier et Backes, 2008). Certains auteurs font référence au terme semi-variogramme à cause du facteur 2 au dénominateur de l’équation de la section suivante (semi comme la moitié du variogramme). Pourtant, ce facteur 2 est utilisé parce que la variance est calculée deux fois pour chaque paire d’observations (pour la paire (i,j) et pour la paire (j,i) alors que la variance est la même). Pour simplifier les choses, les deux termes seront utilisés de manière équivalente. Le variogramme est un outil largement utilisé qui a été créé en premier lieu pour décrire la corrélation spatiale entre observations spatiales. En d’autres termes, on cherche à évaluer si les valeurs attributaires des observations ont une organisation particulière dans l’espace, c’est à dire si elles suivent un patron spatial particulier.
Par exemple, un agriculteur pourrait vouloir savoir si les caractéristiques chimiques du sol à l’intérieur de ses parcelles (ex : matière organique ou teneur en phosphore) présentent une organisation bien structurée dans l’espace ou non. Si une parcelle est bien structurée spatialement, il pourrait être intéressant d’envisager une application modulée dans la parcelle (par exemple une fertilisation minérale).
Le semi-variogramme est la première étape vers la cartographie d’une variable sur toute l’étendue d’une parcelle ou de manière plus générale sur une entité spatiale. Ce processus de cartographie est aussi connu sous le nom d’interpolation. En effet, pour des raisons pratiques et de visualisation, il est beaucoup plus intéressant d’avoir à disposition une cartographie complète de la variable d’intérêt plutôt que des observations spatiales ponctuelles. Une remarque importante : le semi-variogramme n’est pas fiable lorsque le nombre d’observations à disposition est trop faible.
Calcul de la semi-variance
Le semi-variogramme est défini par l’équation suivante :
\gamma(h)=\dfrac{1}{2N(h)}\sum_{i,j\in{N(h)}}(z_i-z_j)^{2}Où N(h) est le nombre de pairs d’observations (i,j) séparées par une distance spatiale h. Les termes z_i et z_j sont les valeurs attributaires des observations i et j respectivement.
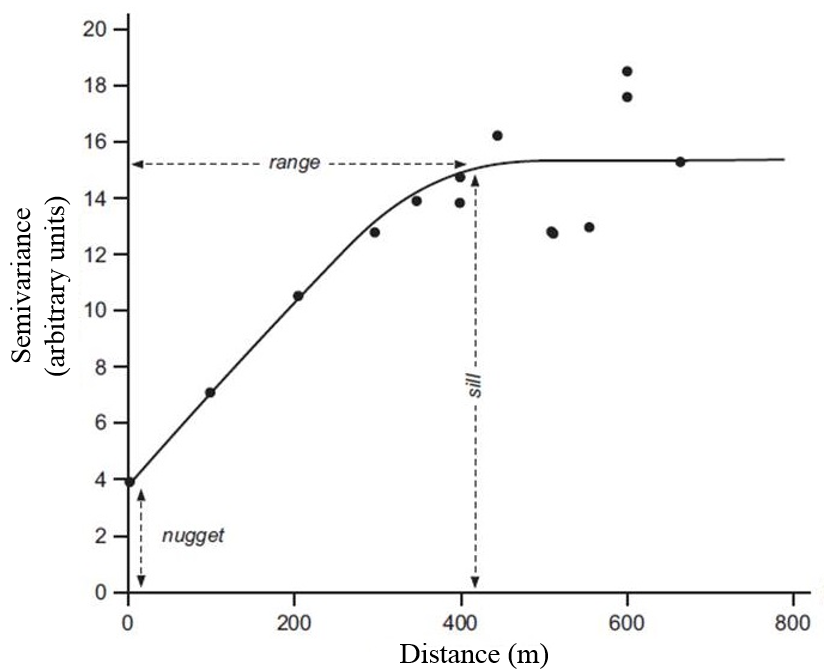
Figure 1. Variogramme expérimental (points) et modèle ajusté au variogramme expérimental (courbe). Le “range”, “nugget”, et “sill” sont les paramètres du variogramme (voir section suivante) et sont traduits par les termes suivants “portée”, “effet pépite” et “pallier”
La fonction calcule la différence attributaire entre des données voisines séparées par une distance h pour évaluer si ces observations présentent une information similaire. Comme il l’a été précisé dans un post précédent, les données agronomiques sont généralement auto-corrélées spatialement. Par rapport au semi-variogramme, cela signifie qu’à mesure que la distance spatiale entre les observations augmente, la semi-variance augmentera probablement aussi parce que des observations proches dans l’espace sont plus susceptibles de partager des caractéristiques similaires que des observations éloignées (Fig. 1). Sur la Figure 1, les points noirs résument la spatiale structure de l’ensemble du jeu de données. En fait, le semi-variogramme est calculé pour toutes les paires d’observations mais la figure aurait été illisible si toutes les semi-variances y avaient été reportées. Une des plus fortes hypothèses du variogramme est celle de stationarité d’ordre 2, c’est à dire le fait fait que le variogramme soit borné et atteigne un plateau. Pour en savoir plus sur les hypothèses fondatrices du semi-variogramme, suivez le guide ! A partir de la fonction de semi-variance, plusieurs paramètres peuvent être déduits pour bien décrire la structure spatiale des observations dans les parcelles.
Les paramètres du variogramme
L’effet pépite, souvent appelé C_0, représente les variations spatiales à petite échelle au sein de parcelles. Ce paramètre indique à quel point la structure spatiale est bruitée. Par exemple, dans les parcelles, il existe de la variabilité naturelle plante à plante parce toutes les plantes voisines ne peuvent pas être exactement identiques. Quand la distance minimale entre des observations voisines est trop grande, il est possible que l’effet nugget soit plus fort que ce qu’il devrait être. Ceci est dû au fait que le semi-variogramme n’est pas capable de capturer l’ensemble de la structure spatiale dans la parcelle, et ce surtout à petite échelle. Il doit être rappelé que les variations à petite échelles peuvent être causées par des erreurs de mesure, et plus spécifiquement par des mesures manuelles, capteurs piétons ou embarqués entre autres. Le pallier partiel, C_1, représente l’amplitude de variation de la variable d’intérêt c’est la différence entre le “sill” et le “nugget” sur la Figure 1). Intuitivement, plus le pallier partiel est important par rapport à l’effet pépite, plus la structure spatiale est forte. Le pallier est la variance du jeu de données et peut être calculé comme la somme de l’effet pépite et du pallier partiel. Le pallier correspond à la valeur obtenue quand la semi-variance atteint un soit-disant “pallier” et se stabilise. Le dernier paramètre mais pas des moindres, la portée, a, est la distance spatiale à partir de laquelle les observations ne sont plus auto-corrélées. Il peut être considéré, qu’en moyenne, au-dessus d’une distance spatiale particulière (la portée), et quelle que soit la paire de points examinée, les observations sont trop différentes et ne partagent pas de relations entre elles.
Pour mieux caractériser la spatiale structure des jeux de données décrits plus hauts, il est nécessaire d’ajuster des fonctions connues au semi-variogramme. Ces fonctions vont permettre d’apporter une description objective de la corrélation spatiale des données étudiées et de récupérer les paramètres précédemment évoqués, C_0, C_1 et a.
Ajustement d’un modèle de semi-variogramme aux données
Avant de décrire les modèles connus de semi-variogramme, il doit être clair que tous les modèles sont théoriques, ce qui veut dire qu’il y a un forte probabilité que les modèles ne puissent pas s’ajuster parfaitement aux données réelles étudiées.
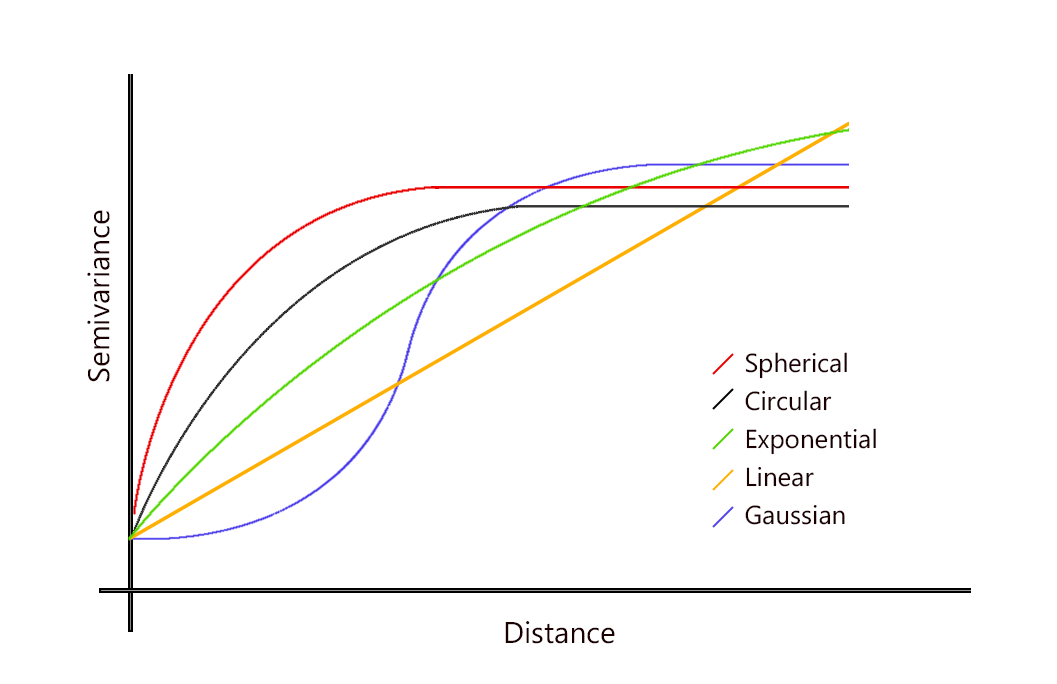
Figure 2. Modèles théoriques de semi-variogramme les plus utilisés
La figure 2 montre les modèles de variogramme les plus utilisés. Dans les études agronomiques, les modèles théoriques sphériques et exponentiels sont les plus employés pour s’ajuster aux données édaphiques (ex: la teneur en nutrient des sols) et aux paramètres des plantes (ex: vigueur, biomasse…). Pour ces deux modèles, l’effet pépite et la portée partielle sont relativement faciles à déterminer. Comme il l’a été précisé précédemment, la portée est la distance à partir de laquelle les observations ne sont plus auto-corrélées, c’est à dire quand la semi-variance atteint un plateau. D’un point de vue théorique, la semi-variance n’atteint jamais ce plateau mais tend plutôt vers ce dernier. Est ce que cela signifie que la portée ne peut pas être définie ? Non, bien évidemment. Plutôt qu’une portée théorique, une portée pratique a été définie pour répondre à ce problème.
Par exemple, pour le modèle exponentiel, la portée pratique est définie comme la distance à partir de laquelle la semi-variance atteint 95% du plateau théorique.
Les modèles de variogramme linéaire ont tendance à croitre indéfiniment. Ces modèles sont souvent le signes de la présence d’une tendance dans les données.
Par exemple, dans le cas d’un gradient d’altitude (sur une pente par exemple), l’altitude augmente dans la direction du gradient ce qui signifie qu’il y a une tendance en relation avec les coordonnées spatiales des observations. Cette tendance devrait être d’abord supprimée avant d’évaluer la vraie structure spatiale de la variable “altitude”.
Un des modèles non présentés ici est un modèle caractérisé par un effet pépite pur (une ligne droite horizontale, la variance est la même quelle que soit la distance entre observations voisines). Dans ce cas, il n’y a absolument aucune structure spatiale, le processus est totalement aléatoire. Il y a soit trop de bruit dans les données ou la variable ne présente effectivement aucune corrélation spatiale.
Jusqu’à présent, toutes les structures qui ont été présentées étaient relativement simples. Encore une fois, tous ces modèles sont théoriques et les fonctions réelles de semi-variance s’écartent généralement de ces modèles. Dans certains cas, il est possible d’avoir à ajuster des modèles imbriquées (modèles gigognes) aux données (Fig. 3). En fait, il est possible qu’il y ait plusieurs structures spatiales au sein d’une même parcelle, et ce à des échelles différentes.
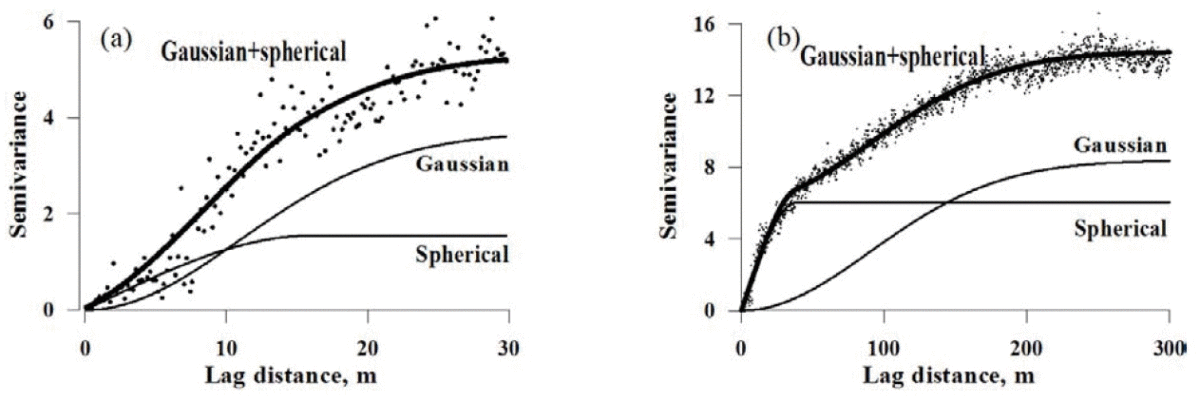
Figure 3. Modèle gigogne de semi-variogramme avec deux structures spatiales
Semi-variogrammes isotopiques et anisotropiques
Un phénomène isotopique est un processus qui n’est pas dépendant d’une direction en particulier. Dans les études spatiales, il est considéré que ce processus évolue de la même façon dans toutes les directions de l’espace. Au contraire, un phénomène anisotropie s’apparente à un processus qui varie de manière différente en fonction de la direction étudiée.
Imaginez par exemple que vous vouliez réaliser une analyse de la diversité des espèces le long d’une pente. Il y a une forte probabilité que les différences de diversité d’espèces soient plus fortes lorsque les altitudes sont différentes que lorsqu’elles sont équivalentes. Les résultats sont susceptibles d’être beaucoup plus intéressants si l’analyse est réalisée dans la direction de la pente. Dans ce cas, l’utilisation d’un variogramme directionnel serait recommandée.
Quelquefois, les modèles anisotropiques permettent de mettre en avant des conclusions qui n’auraient pas été trouvées avec un modèle isotopique de variogramme.
Dernières remarques et discussion
Le semi-variogramme est un outil vraiment intéressant pour analyser la structure spatiale des données spatiales agronomiques et environnementales. Pourtant, certains enjeux doivent être discutés pour éviter des mauvaises interprétations et un usage inapproprié du semi-variogramme. Premièrement, il faut garder à l’esprit que le choix du modèle de variogramme à ajuster aux données conditionne la valeur des paramètres du variogramme (portée, effet pépite et pallier).
Par exemple, sur le même jeu de données, un modèle exponentiel de semi-variogramme conduira à une portée pratique plus faible qu’avec un modèle sphérique
Il est possible de calculer des mesures de qualité d’ajustement pour aider à choisir le meilleur modèle de variogramme mais quand plusieurs modèles sont susceptibles d’être utilisés, il faut être vigilant. Aussi, en fonction de la manière dont la semi-variance est moyennée sur des distances spatiales spécifiques (par exemple, moyennée sur des distances de 5, 20 ou 50m), le semi-variogramme peut avoir une forme différente. Pour toutes ces raisons, je recommanderais de toujours superviser manuellement l’étude variographique. Selon moi, l’automatisation complète des analyses variographiques peut conduire à des conclusions erronées.
Le semi-variogramme est relativement facile à construire (plusieurs packages R sont disponibles, voir ce post!). Encore une fois, j’aimerais attirer l’attention sur le fait que la construction du semi-variogramme nécessite d’avoir un minimum d’observations à disposition. Quand le nombre d’observations est trop faible (<40-50), la fonction de semi-variance n’est pas fiable.
Quelquefois, il arrive de trouver dans la littérature certaines analyses variographiques de paramètres du sol réalisées avec entre dix et vingt échantillons (et même parfois moins). C’est compréhensible parce que l’échantillonnage de sols est relativement coûteux et pénible. Pourtant, la construction d’un semi-variogramme avec dix observations n’a pas vraiment de sens.
Dans l’introduction, le semi-variogramme a été présenté comme la première étape conduisant à l’interpolation de la variable étudiée sur la totalité d’une parcelle. Le semi-variogramme peut aussi être utilisé pour estimer la distance optimale d’échantillonnage entre observations.
Par exemple, une image de NDVI pourrait être utilisée pour estimer la distance spatiale entre observations à choisir pendant une campagne de terrain d’échantillonnage de sols.
Une règle d’or est de considérer que la moitié de la portée pratique du semi-variogramme est un bon indicateur de la distance d’échantillonnage entre observations.
Comme vous l’avez certainement compris, la semi-variance est calculée pour différentes distances spatiales entre observations. Pour obtenir le meilleur variogramme possible, il est nécessaire d’avoir le plus de distances différentes possibles entre observations. Un schéma possible d’échantillonnage serait de ne pas collecter les échantillons régulièrement sur la parcelle dans l’objectif caractériser l’ensemble de la structure spatiale dans les parcelles (Fig. 4)
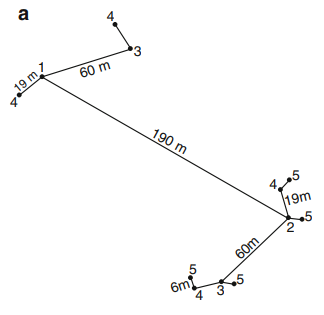
Figure 4. Exemple d’échantillonnage spatial non régulier
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

