Nous allons travailler ici sur un jeu de données assez connu en analyse spatiale – le jeu de données « meuse » – de manière à réintroduire un certain nombre de concepts à ceux qui voudraient se lancer dans de la modélisation linéaire de données spatialisées et dans de l’interpolation spatiale. Ce cas d’étude sera traité sous le language R.
Un des gros intérêt du jeu de données « meuse » est qu’il est directement disponible dans le package sp de R. Il suffit donc de charger le package pour pouvoir récupérer ensuite les données associées. Le jeu de données « meuse » contient la concentration en métaux lourds (zinc, cuivre, plomb, et cadmium) dans la couche supérieure du sol d’une plaine inondable le long de la Meuse. Une des hypothèses est que les sédiments pollués par ces métaux lourds sont transportés par la rivière et se déposent principalement près de la rive, et les zones de faible altitude. C’est ce que nous allons essayer de modéliser dans ce cas d’étude, en s’intéressant notamment au zinc.
[sourcecode language= »r »]
library(sf)
library(sp)
data(meuse) ## loading data
meuse = st_as_sf(meuse,coords=c(« x », »y »),remove=FALSE) ## transforming data frame into sf object
summary(meuse)
[/sourcecode]
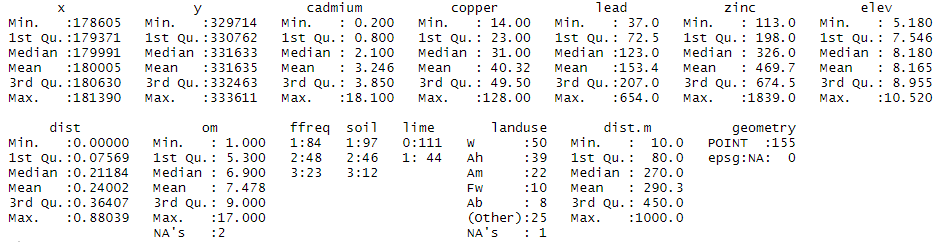
Figure 1. Statistiques descriptives du jeu de données meuse. Les attributs disponibles en plus des quatre métaux lourds sont : « elev » (altitude du terrain), « dist » (la distance à la rivière Meuse normalisée entre 0 et 1), « om » (la teneur en matière organique du sol), « ffreq » (la fréquence d’inondation), « soil » (le type de sol), « lime » (la classe de chaux ou présence de calcaire), « landuse » (l’utilisation du sol), « dist.m » (la distance à la rivière Meuse en mètres). Je vous invite à taper la ligne de commande suivante ‘help(data(« meuse »))’ pour avoir plus d’information sur chacune de ces variables.
Le jeu de données « meuse » contient un ensemble de 155 points d’échantillonnage pour lesquels on dispose de variables quantitatives (concentrations en métaux lourds, élévation et distances à la rivière Meuse, teneur en matière organique du sol) et de variables qualitatives (le reste des variables).
Petits rappels de modélisation linéaire :
L’objectif de ce petit cas d’étude est d’expliquer la distribution de la concentration en zinc sur le site. Nous nous cantonnerons spécifiquement à la modélisation linéaire (c’est l’idée de ce post) pour ne pas s’éparpiller. En fonction du type de variables utilisées pour expliquer le comportement de la variable « zinc », plusieurs choix s’offrent à nous :
- Modèle linéaire simple : Une seule variable quantitative est utilisée en entrée du modèle
- Modèle linéaire multiple : Plusieurs variables quantitatives sont utilisées en entrée du modèle
- One-way ANOVA : Une seule variable qualitative est utilisée en entrée du modèle
- Two-ways ANOVA : Deux variables qualitatives sont utilisées en entrée du modèle
- Multiple-ways ANOVA : Plus de deux variables qualitatives sont utilisées en entrée du modèle
- ANCOVA : Au moins une variable quantitative ET une variable qualitative sont utilisées en entrée du modèle
L’utilisation d’une modélisation linéaire des données n’est pas triviale. Des hypothèses fortes doivent être vérifiées en sortie de modèle pour être sûr que les coefficients de la modélisation linéaire soient robustes et ainsi que ce modèle soit utilisé à des fins explicatives et/ou prédictives. Ces hypothèses sont les suivantes :
- Une relation linéaire doit exister entre la variable explicative et la variable à prédire. Cette hypothèse peut sembler évidente mais elle est très importante à considérer
- Les résidus du modèle doivent suivre une distribution normale
- Les résidus du modèle doivent être homoscédastiques, c’est-à-dire que la variance des résidus doit être stable pour chacune des variables d’entrée utilisées
- Les résidus du modèle doivent être indépendants les uns des autres
Nous y reviendrons dans la suite de ce cas d’étude.
Voyons maintenant à quoi ressemble le jeu de données spatial quand on le présente sur une carte
[sourcecode language= »r »]
data(meuse.grid) ## loading gridded data
coordinates(meuse.grid) = c(« x », « y »)
meuse.grid = as(meuse.grid, « SpatialPixels ») ## transform gridded data into Spatial Pixels
data(meuse.riv) ### loading river data
meuse.lst = list(Polygons(list(Polygon(meuse.riv)), »meuse.riv »))
meuse.sr = SpatialPolygons(meuse.lst) ## concatenate all polygons of the river to reconstruct it entirely
image(meuse.grid, col = « lightgrey »)
plot(meuse.sr, col = « grey », add = TRUE) ## plot the river data
plot(meuse[,c(‘zinc’)], add = TRUE, cex=1.5) ## plot the zinc dataset
title(« Meuse dataset ») ## set the title of the plot
[/sourcecode]
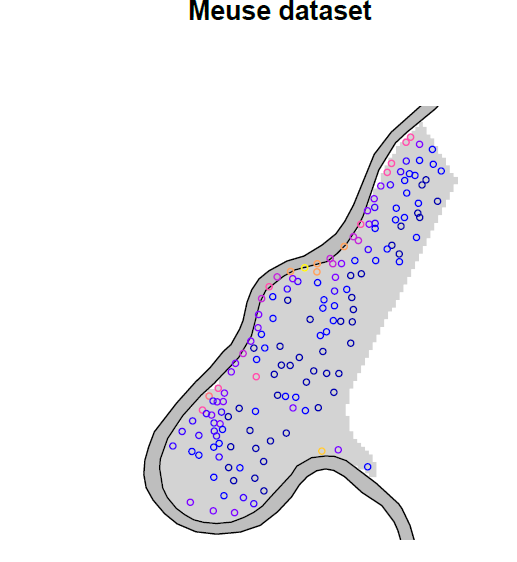
Figure 2. La concentration de zinc sur la plaine inondable le long de la rivière Meuse.
Nous voyons donc la sinueuse rivière Meuse, et – comme exprimé en introduction – il semblerait que les concentrations de zinc soient plus forte le long de la rivière.
Une des premières choses à faire dans toute étude exploratoire est de visualiser les données de manière à évaluer comment considérer le problème.
[sourcecode language= »r »]
library(GGally)
st_geometry(meuse) = NULL ## Transforming back the sf object into a data frame
ggpairs(meuse[,3:9]) ## print correlations between quantitative variables
[/sourcecode]
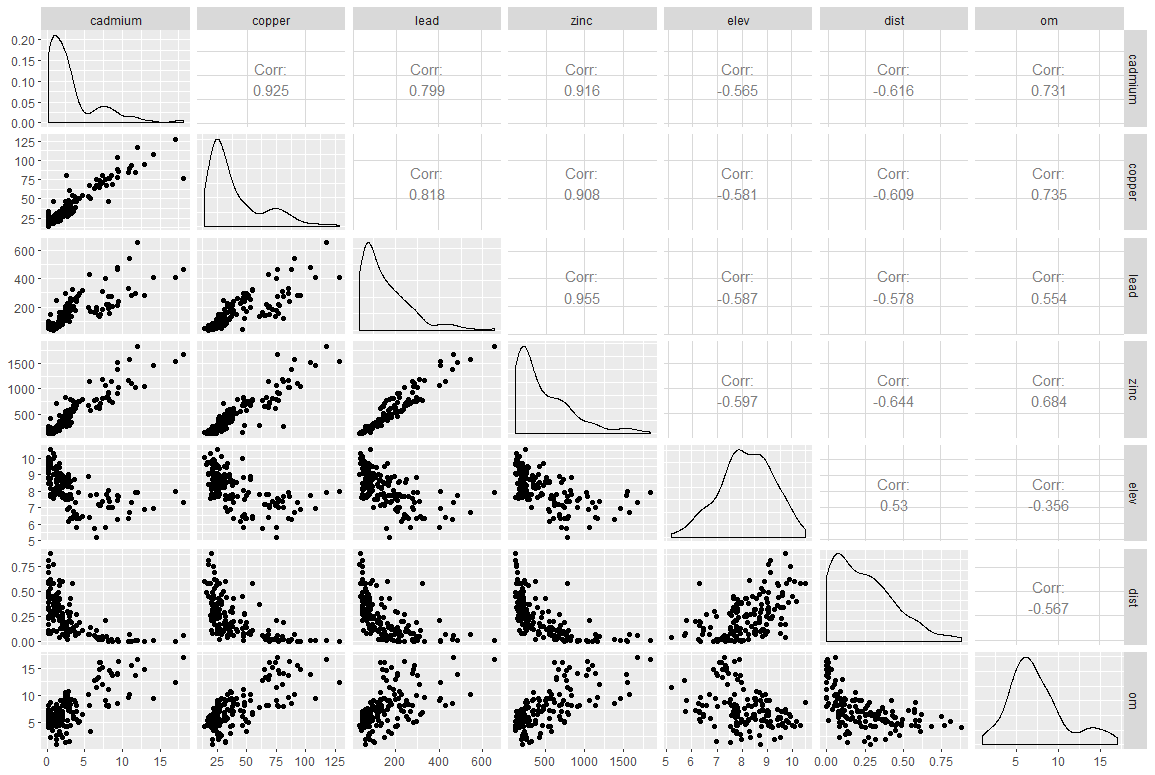
Figure 3. Corrélations entre variables quantitatives dans le jeu de données meuse
La figure 3 nous montre déjà que les concentrations des quatre métaux lourds sur le site sont très fortement corrélés entre elles (valeurs de corrélations de Pearson à plus de 0.8), ce qui n’est pas forcément surprenant). La corrélation entre variables se lit en diagonale sur la figure. Par exemple, la corrélation entre les concentrations en cadmium et cuivre est de 0.925. Celle entre les concentrations en cadmium et zinc est de 0.916. Pour rappel, nous nous focalisons ici sur la concentration en zinc. Nous faisons ici face à un problème de multi-collinéarité, c’est-à-dire que plusieurs des variables qui pourraient être utilisées pour expliquer la distribution des concentrations de zinc sont corrélées entre elles. Considérer ces variables ensemble conduirait à obtenir des coefficients très biaisés dans le modèle. Nous n’aurions de toute façon pas cherché à expliquer la concentration de zinc avec d’autres concentrations en métaux lourds (ça n’aurait pas beaucoup de sens) mais ce problème de multi-collinéarité doit être considéré très sérieusement. En s’intéressant toujours au zinc, on se rend compte que les relations avec le reste des variables quantitatives (elev, dist, et om) ne sont pas si linéaires que ça (je rappelle qu’une des hypothèses fortes de la modélisation linéaire est d’avoir une relation linéaire entre les variables explicatives et la variable à expliquer). Regardons-y un peu de plus près.
[sourcecode language= »r »]
library(cowplot)
plot_grid(
ggplot(meuse, aes(y = zinc, x = elev)) + geom_point(),
ggplot(meuse, aes(y = log(zinc), x = elev)) + geom_point(),
nrow = 1, ncol = 2)
plot_grid(
ggplot(meuse, aes(y = zinc, x = dist)) + geom_point(),
ggplot(meuse, aes(y = log(zinc), x = dist)) + geom_point(),
ggplot(meuse, aes(y = log(zinc), x = sqrt(dist))) + geom_point(),
nrow = 1, ncol = 3)
[/sourcecode]
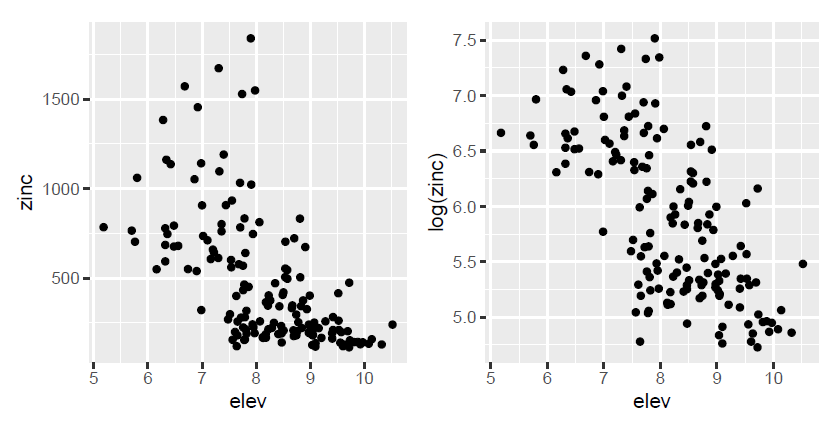
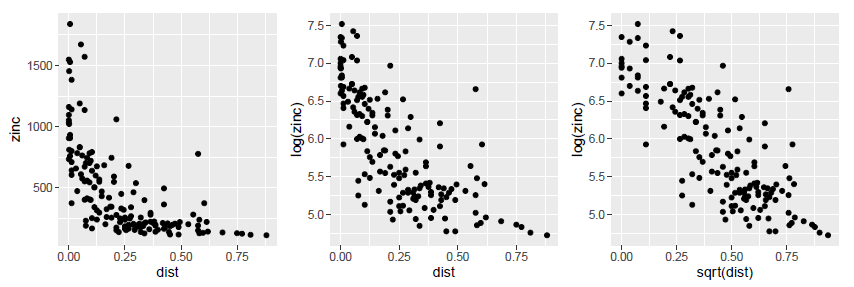
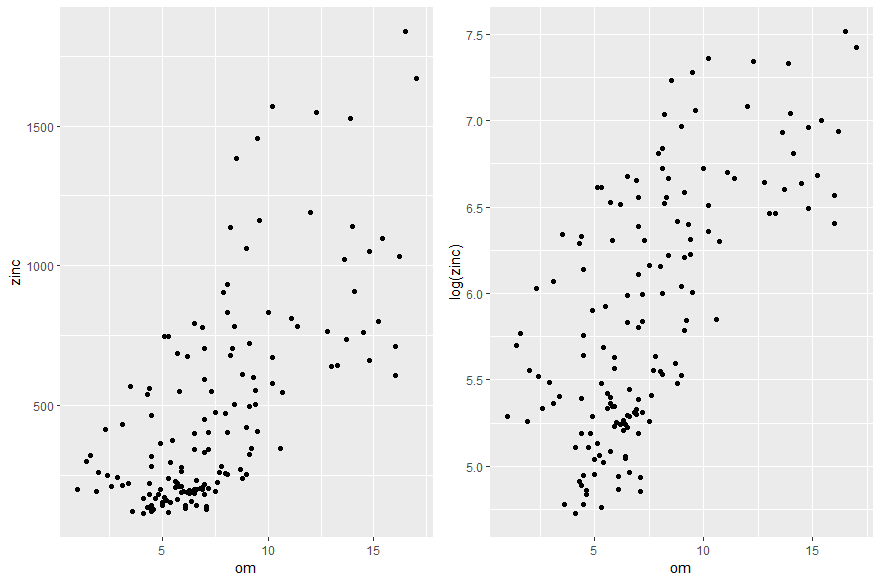Figure 4. Etude des relations entre la concentration en zinc d’une part, et l’altitude du terrain et la distance à la rivière Meuse et la teneur en matière organique du sol d’autre part.
En zoomant sur les graphiques, on se rend effectivement compte que l’hypothèse d’une relation linéaire entre la concentration en zinc d’une part, et l’altitude du terrain et la distance à la rivière Meuse d’autre part, est difficilement justifiable… Pour résoudre ce problème, une des solutions consiste à transformer les variables (transformation logarithmique, transformations carrées etc…) pour faire apparaitre des relations linéaires et assumer l’hypothèse principale de la modélisation. Après transformation des variables, on se rend compte qu’au lieu de chercher à expliquer la concentration en zinc, il serait plus judicieux d’expliquer la log concentration en zinc, parce qu’elle semble reliée linéairement à l’altitude du terrain, et au carré de la distance à la rivière Meuse. Pour la variable teneur en matière organique du sol, la relation linéaire avec la log concentration du zinc est un peu grossière mais pourrait être envisagée.
Jetons maintenant un coup d’œil aux relations entre la concentration en zinc et les variables qualitatives disponibles dans le jeu de données
[sourcecode language= »r »]
plot_grid(
ggplot(meuse, aes(y = log(zinc), x = ffreq)) + geom_boxplot(),
ggplot(meuse, aes(y = log(zinc), x = soil)) + geom_boxplot(),
ggplot(meuse, aes(y = log(zinc), x = lime)) + geom_boxplot(),
ggplot(meuse, aes(y = log(zinc), x = landuse)) + geom_boxplot(),
nrow = 2, ncol = 2)
[/sourcecode]
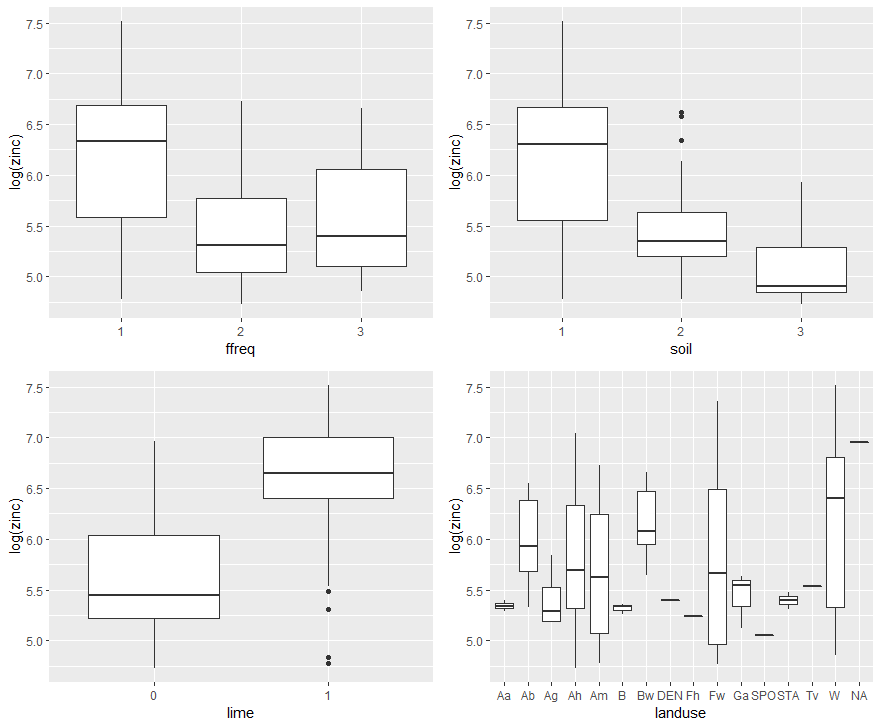
Figure 5. Etude des relations entre la concentration en zinc d’une part, et les variables qualitatives fréquence d’inondation, type de sol, classe de chaux et utilisation du sol.
On observe ici une bonne discrimination de la log concentration en zinc sur trois variables qualitatives – fréquence d’inondation, type de sol et classe de chaux. Il semble y avoir des disparités aussi suivant l’usage des sols mais, à y regarder de plus près, un des gros soucis avec cette variable d’utilisation du sol, est la quantité de modalités présente. Pour certaines modalités, il y a extrêmement peu de points d’échantillonnage ! Un coup d’œil avec la fonction « table » permet de s’en rendre vite compte….
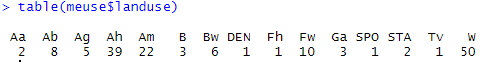
On se retrouve alors face à un problème de déséquilibre entre groupes et de groupes de petite taille. Une des façons de résoudre ce problème pourrait être de réduire le nombre de groupe totaux par classification, en cherchant par exemple à regrouper l’ensemble des occupations du sol dans les trois groupes majoritaires présents (Ah, Am, et W). Pour des raisons de simplicité ici, nous n’allons simplement plus considérer cette variable d’occupation du sol pour expliquer la concentration en zinc sur notre site d’étude.
Modélisation linéaire
Au vu cette étude préliminaire, il reste donc trois variables quantitatives (l’altitude du terrain, la distance à la rivière au carré, la teneur en matière organique) et trois variables qualitatives (la fréquence d’inondation, le type de sol, et la présence ou non de calcaire) pour tenter d’expliquer la concentration en zinc sur la plaine d’étude. Après quelques études annexes, il apparait également :
- qu’il n’y a pas de calcaire dans les classes de sol 2 et 3. Sur ces deux variables qualitatives pédologiques, nous ne retiendrons donc que celle concernant le type de sol.
- Le type de sol est très liée à la distance à la rivière ; nous ne considérerons que la distance à la rivière au carré et pas le type de sol
- La fréquence d’inondation n’est pas totalement liée à la distance à la rivière (assez étrangement au premier abord), cette variable est donc maintenue dans la modélisation également
Au vu des variables à la fois quantitatives et qualitatives utilisables, c’est donc un modèle sous la forme d’une ANCOVA qui est mis en place. Aucune interaction entre variables n’est considérée dans ce cas d’étude.
[sourcecode language= »r »]
library(tidyr)
meuse=meuse %>% drop_na() ## Remove NA variables
Model1=lm(log(zinc)~elev+sqrt(dist)+om+ffreq,data=meuse)
anova(Model1)
[/sourcecode]
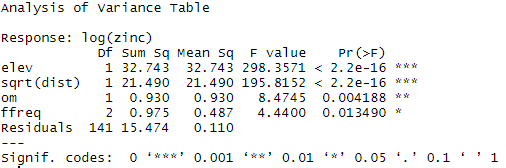
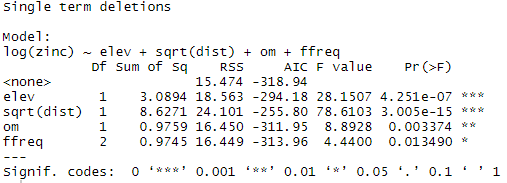
On observe ici que toutes les variables inclues dans le modèle ont un impact significatif sur la log concentration en zinc. Les résultats de la fonction drop1 montrent que la suppression d’une des variables n’est pas nécessaire. Ca pourrait être le cas pour des raisons logistiques ou de compréhension du modèle ; mais nous allons dans notre cas considérer ces variables comme utiles.
[sourcecode language= »r »] drop1(Model1, . ~ ., test= »F ») [/sourcecode]
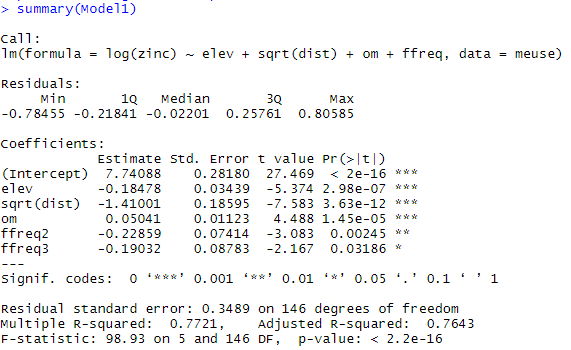
Les coefficients du modèle sont ensuite extraits avec la fonction summary:
[sourcecode language= »r »]
summary(Model1)
[/sourcecode]
Il reste maintenant à s’assurer des quatre hypothèses du modèle linéaire que nous avons formulé au départ. Ces hypothèses peuvent être étudiées au travers des graphiques de diagnostic suivants :
[sourcecode language= »r »]
par(mfrow = c(2, 2))
plot(Model1)
[/sourcecode]
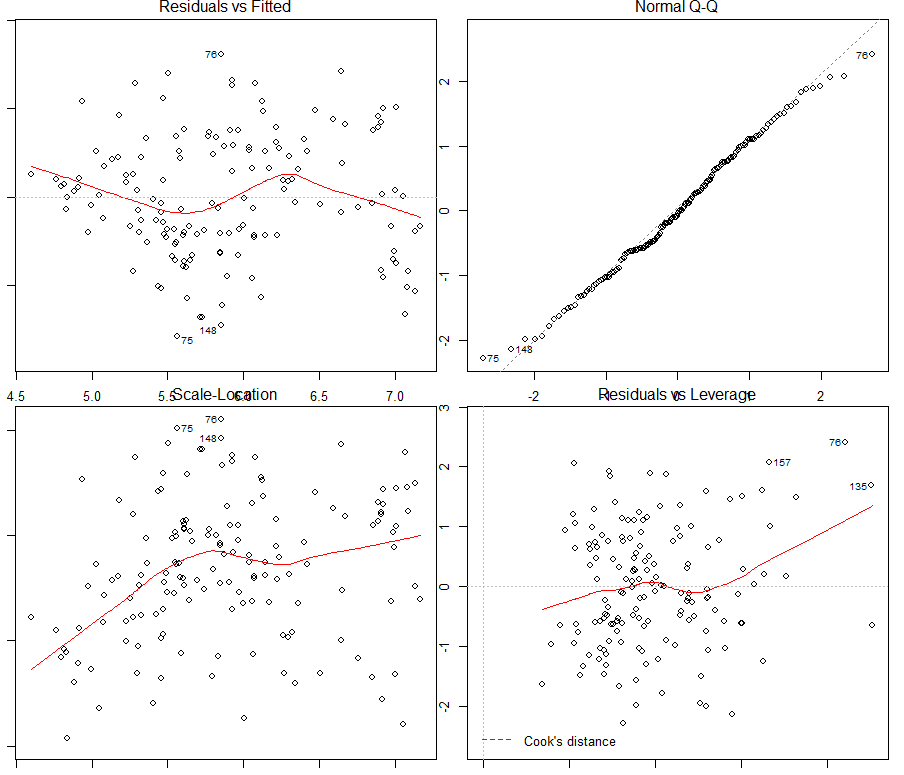
Figure 6. Vérification des hypothèses faites sur le modèle linéaire
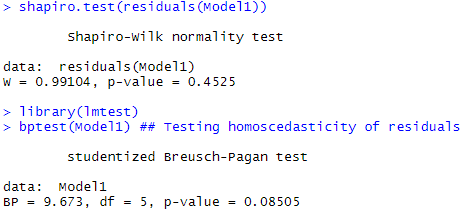
Le premier quadrant de la figure 6 permet de voir que l’hypothèse de linéarité entre la log concentration en zinc et les variables explicatives utilisées peut être assumée (il n’y a pas de patrons spécifiques). De la même façon, l’hypothèse de normalité des résidus semble viable à la vue du second quadrant (un test de shapiro le confirmera juste après – l’hypothèse de normalité ne pouvant pas être rejetée). Dans le troisième quadrant, l’hypothèse d’homoscédasticité des résidus semble être à la limite de la validité, une tendance semblant s’immiscer dans les données (un test de Breusch Pagan confirmera de justesse l’homoscédasticité des résidus -l’hypothèse H0 d’homoscédasticité ne pouvant être rejetée).
Le code suivant présente les résultats des tests de shapiro et Breusch Pagan sur les résidus.
[sourcecode language= »r »]
shapiro.test(residuals(Model1)) ## Testing normality of residuals
library(lmtest)
bptest(Model1) ## Testing homoscedasticity of residuals
[/sourcecode]
Le dernier quadrant fait apparaitre quelques données aberrantes dans le jeu de données, notamment les observations n°76, 157, et 135. On pourra y rajouter les observations n°75 et 148 à la vue des autres quadrants. En affichant ces données influentes sur une carte, il ne semble pas que ces données soient localisées à un endroit spécifique sur le site d’étude. Une étude plus approfondie pourrait néanmoins être menée pour comprendre pourquoi ces observations sont influentes
[sourcecode language= »r »]
Outliers=which(row.names(meuse)%in%c(« 75″, »76″, »135″, »148″, »157 »))
data(meuse) ## loading data
meuse = st_as_sf(meuse,coords=c(« x », »y »),remove=FALSE) ## transforming data frame into sf object
data(meuse.grid)## loading gridded data
coordinates(meuse.grid) = c(« x », « y »)
meuse.grid = as(meuse.grid, « SpatialPixels ») ## transform gridded data into Spatial Pixels
data(meuse.riv) ### loading river data
meuse.lst = list(Polygons(list(Polygon(meuse.riv)), »meuse.riv »))
meuse.sr = SpatialPolygons(meuse.lst) ## concatenate all polygons of the river to reconstruct it entirely
image(meuse.grid, col = « lightgrey »)
plot(meuse.sr, col = « grey », add = TRUE)  ## plot the river data
plot(meuse[Outliers,c(‘zinc’)], add = TRUE, cex=1.5,col= »black »)  ## plot the zinc dataset
title(« Meuse dataset »)
[/sourcecode]
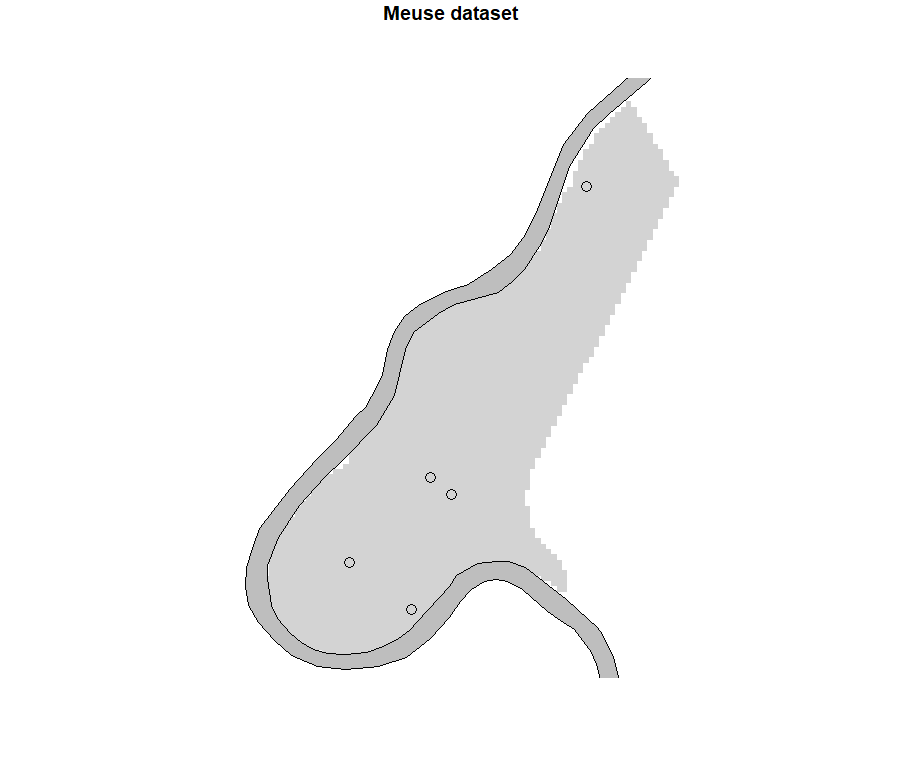
Figure 7. Affichage des données influentes sur la carte
La dernière hypothèse à vérifier reste l’indépendance des résidus. Cette hypothèse peut être évaluée en construisant un variogramme sur ces résidus.
[sourcecode language= »r »]
library(tidyr)
meuse=meuse %>% drop_na() ## Remove NA variables
Model1=lm(log(zinc)~elev+sqrt(dist)+om+ffreq,data=meuse)
meuse$residuals=residuals(Model1)
library(gstat)
Vario_res=variogram(residuals~x+y,data=meuse,cutoff=1200,alpha=c(0,45,90,135))## plotting directional variograms
Vario_res.fit = vgm(.13, « Sph », 1000, .02, anis = c(45, .6)) ## Fitting a model plot(Vario_res,Vario_res.fit)
[/sourcecode]
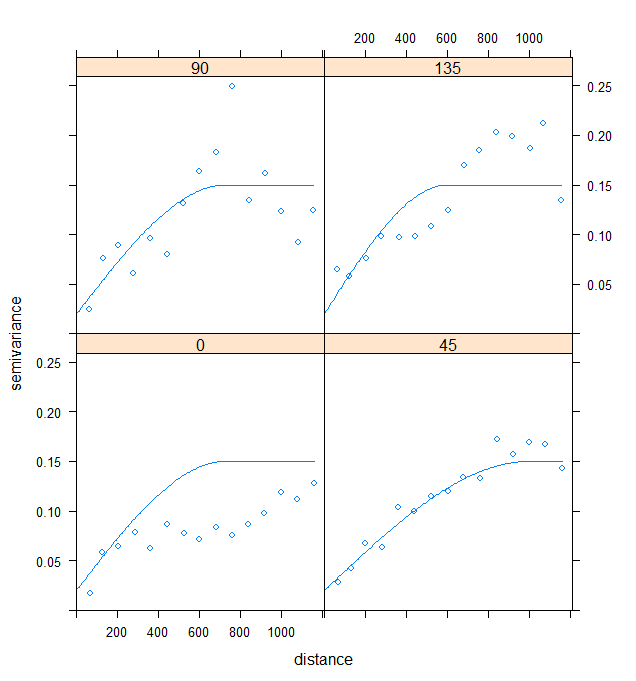Figure 8. Variogrammes directionels des résidus du modèle 1
Ici, le choix d’une modélisation anisotropique de la structure spatiale a été faite au vu de la forme du site d’étude. La plaine étant orientée dans la direction Sud-Ouest/Nord-Est, il n’est pas surprenant que la direction de plus forte structure spatiale soit celle à 45° (c’est-à-dire Nord-Est). Un modèle sphérique a ici été considéré car il paraissait le plus approprié. Ces variogrammes nous montrent surtout que les résidus ne sont pas indépendants et qu’une structure spatiale est encore présente dans les résidus… Nous ne pouvons donc pas avoir une confiance aveugle (le terme est peut-être un peu fort…) dans les coefficients de notre modèle.
Il existe plusieurs façons de considérer cette structure spatiale dans notre modélisation. Nous pouvons soit travailler :
- sous la forme d’un modèle de régression de type « Spatial Lag model », « Spatial Error model », ou une combinaison des deux. Il est nécessaire dans ce cas là de définir des relations de voisinage entre les points, puis de comparer les modèles de régression les plus appropriés aux données.
- ou sous la forme d’une modèle linéaire étendu et ajouter une structure de corrélation dans la modélisation.
C’est cette deuxième option que nous allons choisir ici. L’ajout d’une structure de corrélation spatiale demande de changer de fonction R. Au lieu d’utiliser la fonction classique ‘lm’, nous devons passer par le package ‘nlme’ et la fonction ‘gls’. Notez également que la fonction gls est intéressante dans le sens où il est possible de rajouter d’autres arguments intéressants, notamment pour modéliser l’hétéroscédasticité des résidus si cette dernière est présente.
[sourcecode language= »r »]
library(nlme)
modSpher= gls(log(zinc)~elev+sqrt(dist)+om+ffreq,data=meuse,correlation=corSpher(c(1000, 0.15),form=~x+y,nugget=T)) ## Adding a correlation structure with a spherical form in the modelling
VarioSpher_raw = Variogram(modSpher, form =~ x+y,robust = TRUE, maxDist = 1000, resType = « pearson ») ## variogram of the raw residuals
VarioSpher_normalized = Variogram(modSpher, form =~ x+y,robust = TRUE, maxDist = 1000, resType = « normalized ») ## variogramof the studentized residuals
plot(VarioSpher_raw)
plot(VarioSpher_normalized)
[/sourcecode]
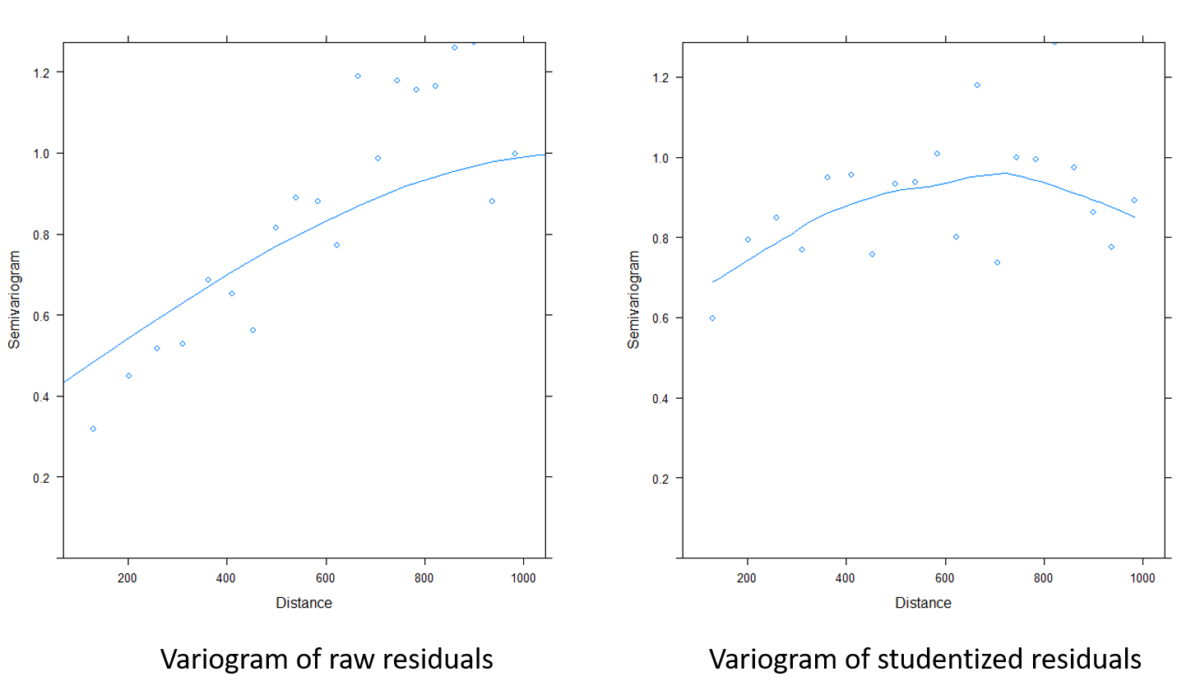
Figure 9. Comparaison des variogrammes sur les résidus du modèle avant prise en compte de la structure spatiale et après l’avoir prise en compte
La figure 9 montre à quel point une bonne partie de la structure spatiale restante dans les résidus a été supprimée. Les coefficients du modèle peuvent donc être extraits et aider à mieux comprendre le comportement de la log concentration du zinc sur le site d’étude. Vous pouvez d’ailleurs observer que ces coefficients sont légèrement différents de ceux obtenus sans la prise en compte de la structure spatiale.
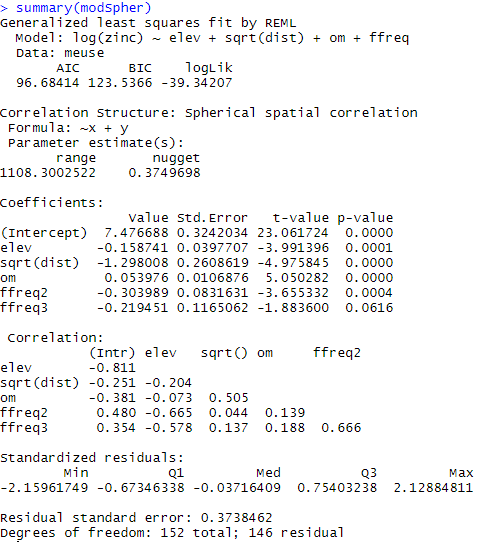
Une fois ce travail réalisé, il reste possible d’interpoler la log concentration de zinc sur le site d’étude. Nous n’irons pas jusque là mais plusieurs options s’offrent à nous :
- Un krigeage ordinaire (« Ordinary kriging ») relativement simple
- Un krigeage universel (« Universal kriging ») en utilisant les coordonnées x/y sur le site d’étude (tendance de surface d’ordre 1, voire 2)
- Un krigeage avec régression (« Regression Kriging ») dans le cas où on aurait une variable continue sur l’ensemble du site d’étude. C’est par exemple le cas avec la distance à la rivière (c’est un paramètre que l’on peut calculer simplement sur l’ensemble d’une grille d’interpolation). On peut imaginer pouvoir aussi créer une carte d’altitude assez précise par interpolation (si les variations d’altitude ne sont pas trop fortes). Un modèle de régression plus simple que le Modèle 1 utilisé dans ce cas d’étude pourrait donc servir à améliorer l’interpolation de la log concentration de zinc.
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?
